题目内容
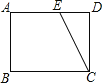
矩形ABCD一条边AD=8，将矩形ABCD折叠，使得点B落在CD边上的点P处．
（1）如图1，已知折痕与边BC交于点O，连接AP、OP、OA．
①求证：△OCP∽△PDA；
②若△OCP与△PDA的面积比为1：4，求边AB的长．
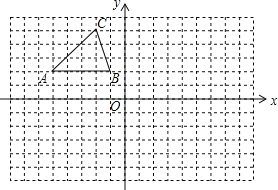
（2）如图2，在（1）的条件下，擦去AO和OP，连接BP．动点M在线段AP上（不与点P、A重合），动点N在线段AB的延长线上，且BN=PM，连接MN交PB于点F，作ME⊥BP于点E．试问动点M、N在移动的过程中，线段EF的长度是否发生变化？若不变，求出线段EF的长度；若变化，说明理由．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
相关题目
根据下面的两种移动电话计费方式，解答下列问题：
方式一 | 方式二 | |
月租费 | 20元/月 | 0 |
本地通话费 | 0.10元/分钟 | 0.20元/分钟 |
(1)对于某本地通话时间，会出现按两种计费方式收费一样的情况吗？
(2)请通过计算说明：什么情况下，使用方式一合算？什么情况下，使用方式二合算？
B. 800+270
