题目内容
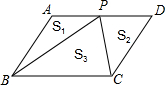 如图,点P为?ABCD的边CD上一点,若△PAB、△PCD和△PBC的面积分别为s1、s2和s3,则它们之间的大小关系是( )
如图,点P为?ABCD的边CD上一点,若△PAB、△PCD和△PBC的面积分别为s1、s2和s3,则它们之间的大小关系是( )| A、S3=S1+S2 | B、2S3=S1+S2 | C、S3>S1+S2 | D、S3<S1+S2 |
分析:设平行四边形的高为h,然后分别表示出s1、s2和s3,即可得出三者的关系.
解答:解:设平行四边形的高为h,
则S1=
×AP×h,S2=
PD×h,S3=
BC×h,
又平心四边形的对边相等,
∴AP+PD=AD=BC,
∴S3=S1+S2.
故选A.
则S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又平心四边形的对边相等,
∴AP+PD=AD=BC,
∴S3=S1+S2.
故选A.
点评:本题考查平行四边形的知识,难度不大,注意掌握平行四边形的底边相等及高相同的三角形的面积正比于其底边.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 12、如图,点H为△ABC的垂心,以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D,延长AD交CH于点P,
12、如图,点H为△ABC的垂心,以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D,延长AD交CH于点P, 25、尺规作图(不写作法,但要保留作图痕迹)
25、尺规作图(不写作法,但要保留作图痕迹)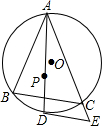 如图,点P为△ABC的内心,延长AP交△ABC的外接圆⊙O于D,过D作DE∥BC,交AC的延长线于E点.①则直线DE与⊙O的位置关系是
如图,点P为△ABC的内心,延长AP交△ABC的外接圆⊙O于D,过D作DE∥BC,交AC的延长线于E点.①则直线DE与⊙O的位置关系是 如图,点G为△ABC的重心,DE过点G,且DE∥BC,EF∥AB,那么CF:BF=
如图,点G为△ABC的重心,DE过点G,且DE∥BC,EF∥AB,那么CF:BF= 如图,点E为△ABC边AB上一点,AC=BC=BE,AE=EC,BD⊥AC于D,求∠CBD的度数.
如图,点E为△ABC边AB上一点,AC=BC=BE,AE=EC,BD⊥AC于D,求∠CBD的度数.