题目内容
已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为1.8元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用,其标准如下:7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.(1)当9天购买一次配料时,分别写出该厂第8天和第9天剩余配料的重量;
(2)当9天购买一次配料时,求该厂用于配料的保管费用P是多少元?
(3)设该厂x天购买一次配料,求该厂在这x天中用于配料的总费用y(元)关于x的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
[提示:
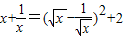 (x>0)].
(x>0)].
【答案】分析:(1)根据题意得出第8天剩余配料的重量=9天配料的重量-7天配料的重量,第9天剩余配料的重量=9天配料的重量-8天配料的重量,分别代入求出即可;
(2)根据题意:7天的费用=70,8、9两天的费用=0.03×200×(1+2),相加求出即可;
(3)①当x≤7时,这x天中用于配料的总费用y=360x+10x+236;②当x>7时,这x天中用于配料的总费用y=360x+236+70+6[(x-7)+(x-8)+…+2+1];求出即可;求出 和
和 的最值即可.
的最值即可.
解答:(1)解:第8天剩余配料200×9-200×7=400(千克),
第9天剩余配料200×9-200×8=200(千克),
答:该厂第8天和第9天剩余配料的重量分别是400千克,200千克.
(2)解:当9天购买一次时,该厂用于配料的保管费用
P=70+0.03×200×(1+2)=88(元),
答:当9天购买一次配料时,求该厂用于配料的保管费用P是88元.
(3)解:①当x≤7时,
y=360x+10x+236=370x+236;
②当x>7时,
y=360x+236+70+6[(x-7)+(x-8)+…+2+1],
=3x2+321x+432.
∴设该厂x天购买一次配料平均每天支付的费用为W元
当x≤7时,W= ,
,
当x>7时,W= ,
,
当x≤7时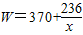 ,当且仅当x=7时,W有最小值
,当且仅当x=7时,W有最小值 (元),
(元),
当x>7时 =
= ,
,
∴当x=12时W有最小值393元,
答:该厂在这x天中用于配料的总费用y(元)关于x的函数关系式是y=370x+236(x≤7)y=3x2+321x+432(x>7),该厂12天购买一次配料才能使平均每天支付的费用最少.
点评:本题主要考查对二次函数的最值,二次函数等知识点的理解和掌握,能根据题意列出算式是解此题的关键.
(2)根据题意:7天的费用=70,8、9两天的费用=0.03×200×(1+2),相加求出即可;
(3)①当x≤7时,这x天中用于配料的总费用y=360x+10x+236;②当x>7时,这x天中用于配料的总费用y=360x+236+70+6[(x-7)+(x-8)+…+2+1];求出即可;求出
 和
和 的最值即可.
的最值即可.解答:(1)解:第8天剩余配料200×9-200×7=400(千克),
第9天剩余配料200×9-200×8=200(千克),
答:该厂第8天和第9天剩余配料的重量分别是400千克,200千克.
(2)解:当9天购买一次时,该厂用于配料的保管费用
P=70+0.03×200×(1+2)=88(元),
答:当9天购买一次配料时,求该厂用于配料的保管费用P是88元.
(3)解:①当x≤7时,
y=360x+10x+236=370x+236;
②当x>7时,
y=360x+236+70+6[(x-7)+(x-8)+…+2+1],
=3x2+321x+432.
∴设该厂x天购买一次配料平均每天支付的费用为W元
当x≤7时,W=
 ,
,当x>7时,W=
 ,
,当x≤7时
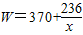 ,当且仅当x=7时,W有最小值
,当且仅当x=7时,W有最小值 (元),
(元),当x>7时
 =
= ,
,∴当x=12时W有最小值393元,
答:该厂在这x天中用于配料的总费用y(元)关于x的函数关系式是y=370x+236(x≤7)y=3x2+321x+432(x>7),该厂12天购买一次配料才能使平均每天支付的费用最少.
点评:本题主要考查对二次函数的最值,二次函数等知识点的理解和掌握,能根据题意列出算式是解此题的关键.

练习册系列答案
相关题目
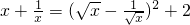 (x>0)].
(x>0)].