题目内容
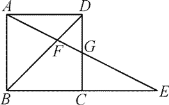
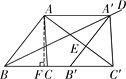
【题目】如图,将△ABC沿射线BC平移得到△A′B′C′,使得点A′落在∠ABC的平分线BD上,连接AA′,AC′.
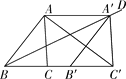
(1)判断四边形ABB′A′的形状,并证明;
(2)在△ABC中,AB=6,BC=4,若AC′⊥A′B′,求四边形ABB′A′的面积.
【答案】(1)四边形ABB′A′是菱形,证明见解析;(2)![]()
【解析】
(1)先根据平移的性质得出四边形ABB′A′是平行四边形,则有∠AA′B=∠A′BC,再通过角平分线的定义通过等量代换得出∠AA′B=∠A′BA,则有AB=AA′,则可证明![]() 是菱形;
是菱形;
(2)过点A作AF⊥BC于点F,设AC′与A′B′交于点E,由AB∥A′B′可得出∠BAC′=∠B′EC′=90°,在Rt△ABC′中利用勾股定理求出AC′的长度,然后利用等面积法求出AF的长度,最后利用S菱形ABB′A′=BB′·AF即可求出答案.
解:(1)四边形ABB′A′是菱形.
证明如下:由平移得AB∥A′B′,AB=A′B′,
∴四边形ABB′A′是平行四边形,
∴∠AA′B=∠A′BC.
∵BA′平分∠ABC,
∴∠ABA′=∠A′BC.
∴∠AA′B=∠A′BA.
∴AB=AA′.
∴![]() 是菱形;
是菱形;
(2)如解图,过点A作AF⊥BC于点F,设AC′与A′B′交于点E.
由(1)得BB′=BA=6.
由平移得△A′B′C′≌△ABC,
∴B′C′=BC=4.
∴BC′=10.
∵AC′⊥A′B′,
∴∠B′EC′=90°.
∵AB∥A′B′,
∴∠BAC′=∠B′EC′=90°.
在Rt△ABC′中,AC′=![]() =8.
=8.
∵S△ABC′=![]() AB·AC′=
AB·AC′=![]() BC′·AF,
BC′·AF,
∴AF=![]() =
=![]() .
.
∴S菱形ABB′A′=BB′·AF=![]() .
.
即四边形SABB′A′的面积是![]() .
.

练习册系列答案
相关题目