题目内容
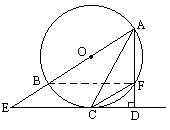
如图,已知C在⊙O上,过点C的切线与直径AB的延长线交于点E,过点A作EC的垂线交直线EC于D,与⊙O交于点F,连结AC、CF.求证:AC2=AE·AF.
答案:
解析:
提示:
解析:
|
证明:连结BF,则∠BFA= ∴BF∥ED. ∴∠E=∠ABF=∠ACF. 又∵∠EAC=∠BFC=∠FCD, 且∠FCD=∠CAF, ∴∠EAC=∠CAF. ∴△AEC∽△ACF. ∴ ∴AC2=AE·AF. |
提示:
|
寻求几何问题证题思路的常用方法是分析法,即假设命题的结论成立,若能由此逐步推导到已知条件或熟知的定理,且这些推理过程是互逆的,那么它的证题思路就算找到了.比如本题,要证AC2=AE·AF成立,因这些线段分别是△AEC和△ACF的对应边,故只须证这两个三角形相似;而要证它们相似,只须证它们有两对对应角相等.至此,问题转化为“证明△AEC和△ACF的对应角相等”.在这些角中,除∠E外,它们都是⊙O的圆周角或弦切角.为便于比较,最好把∠E也转化为圆周角或弦切角,而实现这一转化的最方便做法是作辅助残BF.当然,也可以运用弦切角定理来证明它们另一对较大的角(∠ACE和∠AFC)相等,同样可证明△AEC∽△ACF. |

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
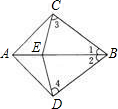
 在直线
在直线 上,点
上,点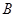 在直线
在直线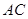 上,若
上,若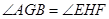 .
.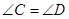 ,则
,则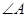 与
与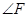 相等吗?为什么?
相等吗?为什么?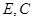 在线段
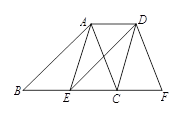
在线段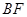 上,
上,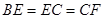 ,
,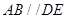 ,
,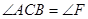 .
.
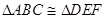 ;
; 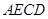 的形状,并证明你的结论.
的形状,并证明你的结论.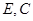 在线段
在线段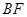 上,
上,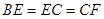 ,
,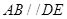 ,
,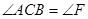 .
.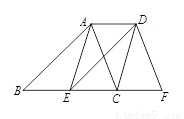
 ;
;  的形状,并证明你的结论.
的形状,并证明你的结论. 在直线
在直线 上,点
上,点 在直线
在直线 上,若
上,若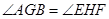 .
.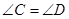 ,则
,则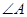 与
与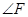 相等吗?为什么?
相等吗?为什么?