题目内容
【题目】已知抛物线y=![]() +mx﹣2m﹣2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,
+mx﹣2m﹣2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,
(1)当m=1时,求点A和点B的坐标;
(2)抛物线上有一点D(﹣1,n),若△ACD的面积为5,求m的值;
(3)P为抛物线上A、B之间一点(不包括A、B),PM⊥x轴于点M,求![]() 的值.
的值.
【答案】(1)A(﹣4,0),B(2,0);(2)![]() ;(3)2.
;(3)2.
【解析】
试题分析:(1)当m=1时,抛物线解析式为y=![]() +x﹣4.然后解方程
+x﹣4.然后解方程![]() +x﹣4=0可得A、B的坐标;
+x﹣4=0可得A、B的坐标;
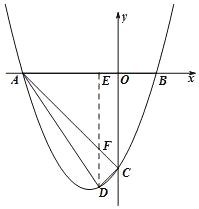
(2)过点D作DE⊥AB于点E,交AC于点F,如图,解方程![]() +mx﹣2m﹣2=0得
+mx﹣2m﹣2=0得![]() =2,
=2,![]() =﹣2m﹣2,则A为(﹣2m﹣2,0),B(2,0),易得C(0,﹣2m﹣2),所以OA=OC=2m+2,则∠OAC=45°.利用D(﹣1,n)得到OE=1,AE=EF=2m+1.n=﹣3m﹣
=﹣2m﹣2,则A为(﹣2m﹣2,0),B(2,0),易得C(0,﹣2m﹣2),所以OA=OC=2m+2,则∠OAC=45°.利用D(﹣1,n)得到OE=1,AE=EF=2m+1.n=﹣3m﹣![]() ,再计算出DF=m+
,再计算出DF=m+![]() ,利用三角形面积公式得到
,利用三角形面积公式得到![]() (m+
(m+![]() )(2m+2)=5.解方程得到
)(2m+2)=5.解方程得到![]() =
=![]() ,
,![]() =﹣3,最后利用m≥0得到m=
=﹣3,最后利用m≥0得到m=![]() ;
;
(3)由(2)得点A(﹣2m﹣2,0),B(2,0).设点P的坐标为(p,q).则AM=p+2m+2,BM=2﹣p,AMBM=![]() ﹣2mp+4m+4,PM=﹣q.再利用点P在抛物线上得到q=
﹣2mp+4m+4,PM=﹣q.再利用点P在抛物线上得到q=![]() +mp﹣2m﹣2,所以AMBM=2 PM,从而得到
+mp﹣2m﹣2,所以AMBM=2 PM,从而得到![]() 的值.
的值.
试题解析:(1)当m=1时,抛物线解析式为y=![]() +x﹣4.
+x﹣4.
当y=0时,![]() +x﹣4=0,解得
+x﹣4=0,解得![]() =﹣4,
=﹣4,![]() =2.
=2.
∴A(﹣4,0),B(2,0);
(2)过点D作DE⊥AB于点E,交AC于点F,如图,
当y=0时,![]() +mx﹣2m﹣2=0,则(x﹣2)(x+2m+2)=0,
+mx﹣2m﹣2=0,则(x﹣2)(x+2m+2)=0,
解得![]() =2,
=2,![]() =﹣2m﹣2,
=﹣2m﹣2,
∴点A的坐标为(﹣2m﹣2,0),B(2,0),
当x=0时,y=﹣2m﹣2,则C(0,﹣2m﹣2),
∴OA=OC=2m+2,
∴∠OAC=45°.
∵D(﹣1,n),
∴OE=1,
∴AE=EF=2m+1.
当x=﹣1时,n=![]() ﹣m﹣2m﹣2=﹣3m﹣
﹣m﹣2m﹣2=﹣3m﹣![]() ,
,
∴DE=3m+![]() ,
,
∴DF=3m+![]() ﹣(2m+1)=m+
﹣(2m+1)=m+![]() ,
,
又∵S△ACD=![]() DFAO.
DFAO.
∴![]() (m+
(m+![]() )(2m+2)=5.
)(2m+2)=5.
![]() +3m﹣9=0,解得
+3m﹣9=0,解得![]() =
=![]() ,
,![]() =﹣3.
=﹣3.
∵m≥0,
∴m=![]() ;
;
(3)点A的坐标为(﹣2m﹣2,0),点B的坐标为(2,0).
设点P的坐标为(p,q).则AM=p+2m+2,BM=2﹣p,
AMBM=(p+2m+2)( 2﹣p)=![]() ﹣2mp+4m+4,
﹣2mp+4m+4,
PM=﹣q.
因为点P在抛物线上,
所以q=![]() +mp﹣2m﹣2.
+mp﹣2m﹣2.
所以AMBM=2PM.
即![]() =2.
=2.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案