题目内容
如图,已知![]() ABCD的周长为60cm,对角线AC、BD相交于点O,△BOC的周长比△AOB的周长小8cm,求AB、BC的长.
ABCD的周长为60cm,对角线AC、BD相交于点O,△BOC的周长比△AOB的周长小8cm,求AB、BC的长.
答案:
解析:
提示:
解析:
|
解:在 ∴2(AB+BC)=60, 即AB+BC=30 ① ∵平行四边形对角线互相平分, ∴AO=CO,BO=DO,(平行四边形的特征) ∴△AOB的周长-△BOC的周长 =(AB+OB+OA)-(BC+OB+OC) =AB+OB+OA-BC-OB-OC =AB-BC=8, ② 由①②,可得:B=19cm,BC=11cm.(方程组的思想) 思路分析:仔细观察图形的组合规律,找出相关线段之间的转化关系是解本题的关键:(1)由平行四边形对边相等,得AB+BC=30;(2)由平行四边形对角线互相平分,得△AOB的周长-△BOC的周长=AB-BC=8,又(1)、(2)联立方程组,问题即可迎刃而解. |
提示:
|
点评:利用方程组的思想解决几何求值问题,是常用的方法.方程组的思想是常用的数学思想方法. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
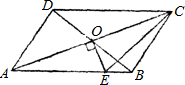 20、如图,已知?ABCD的周长为60cm,对角线AC与BD相交于点O,OE⊥AC交AB于E,则△CEB的周长为
20、如图,已知?ABCD的周长为60cm,对角线AC与BD相交于点O,OE⊥AC交AB于E,则△CEB的周长为
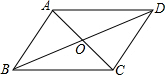 (2013•吴中区二模)如图,已知?ABCD的对角线BD=4cm,将?ABCD绕其对称中心O旋转90°,则点D所转过的路径长为( )
(2013•吴中区二模)如图,已知?ABCD的对角线BD=4cm,将?ABCD绕其对称中心O旋转90°,则点D所转过的路径长为( )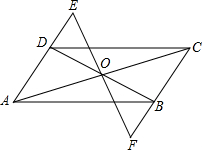 (2002•岳阳)如图,已知?ABCD的对角线AC、BD相交于点O,过点O任作一直线分别交AD、CB的延长线于E、F,求证:OE=OF.
(2002•岳阳)如图,已知?ABCD的对角线AC、BD相交于点O,过点O任作一直线分别交AD、CB的延长线于E、F,求证:OE=OF. 如图,已知?ABCD的对称中心在原点O,且A(-2,1),B(-3,-2)
如图,已知?ABCD的对称中心在原点O,且A(-2,1),B(-3,-2)