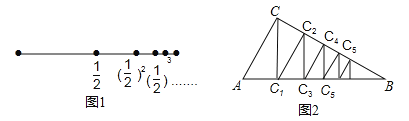��Ŀ����
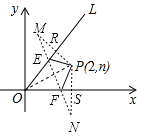
����Ŀ��̽����С������ͬһ�������������ľ���ʱ���֣�����ƽ��ֱ������ϵ����������P1��x1��y1����P2��x2��y2������ͨ������ֱ������������ͼ1�õ����ۣ�![]() ��������ͼ2֤�����߶�P1P2���е�P��x��y��P�����깫ʽ��
��������ͼ2֤�����߶�P1P2���е�P��x��y��P�����깫ʽ��![]() ��
��![]() ��
��
��1�������С��д���е����깫ʽ��֤�����̣�
���ã���2������֪��M��2����1����N����3��5�������߶�MN����Ϊ ��
��ֱ��д���Ե�A��2��2����B����2��0����C��3����1����DΪ�����ƽ���ı��ζ���D�����꣺ ��
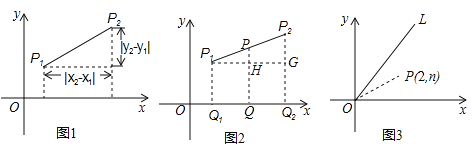
��չ����3����ͼ3����P��2��n���ں���![]() ��x��0����ͼ��OL��x��������нǵ�ƽ�����ϣ�����OL��x���Ϸֱ��ҳ���E��F��ʹ��PEF���ܳ���С����Ҫ������ͼ������������ܳ�����Сֵ��
��x��0����ͼ��OL��x��������нǵ�ƽ�����ϣ�����OL��x���Ϸֱ��ҳ���E��F��ʹ��PEF���ܳ���С����Ҫ������ͼ������������ܳ�����Сֵ��
���𰸡���1���𰸼���������2����![]() ��������3��3����7��1����1����3������3��
��������3��3����7��1����1����3������3��![]() ��
��
��������
�����������1����P1��P2������ֱ��ʾ��OQ��PQ�ij�����֤�ý��ۣ�
��2����ֱ�������������빫ʽ�����MN�ij�������AB��AC��BCΪ�Խ��ߣ�����������ĵ����꣬�������е����깫ʽ�����D�����ꣻ
��3����P����ֱ��OL�ĶԳƵ�ΪM������x��ĶԳƵ�ΪN������PM��ֱ��OL�ڵ�R������PN��x���ڵ�S�����֪OR=OS=2�������������빫ʽ�����R�����꣬����PR=PS=n�������n��ֵ�������P�����꣬�����е����깫ʽ�����M�����꣬�ɶԳ��Կ����N�����꣬����MN��ֱ��OL�ڵ�E����x���ڵ�S����ʱEP=EM��FP=FN����ʱ������PEF���ܳ���С�������������빫ʽ��������ܳ�����Сֵ��
���������
��1����P1��x1��y1����P2��x2��y2������Q1Q2=OQ2��OQ1=x2��x1����Q1Q=![]() ����OQ=OQ1+Q1Q=x1+
����OQ=OQ1+Q1Q=x1+![]() =
=![]() ����PQΪ����P1Q1Q2P2����λ�ߣ���PQ=
����PQΪ����P1Q1Q2P2����λ�ߣ���PQ=![]() =
=![]() �����߶�P1P2���е�P��x��y��P�����깫ʽΪx=
�����߶�P1P2���е�P��x��y��P�����깫ʽΪx=![]() ��y=
��y=![]() ��
��
��2���١�M��2����1����N����3��5������MN=![]() =
=![]() ���ʴ�Ϊ��
���ʴ�Ϊ��![]() ��
��
�ڡ�A��2��2����B����2��0����C��3����1��������ABΪƽ���ı��εĶԽ���ʱ����Գ���������Ϊ��0��1������D��x��y������x+3=0��y+����1��=2�����x=��3��y=3������ʱD������Ϊ����3��3������ACΪ�Խ���ʱ��ͬ�������D������Ϊ��7��1������BCΪ�Խ���ʱ��ͬ�������D������Ϊ����1����3�������Ͽ�֪D������Ϊ����3��3����7��1����1����3�����ʴ�Ϊ������3��3����7��1����1����3����
��3����ͼ����P����ֱ��OL�ĶԳƵ�ΪM������x��ĶԳƵ�ΪN������PM��ֱ��OL�ڵ�R������PN��x���ڵ�S������MN��ֱ��OL�ڵ�E����x���ڵ�F���ֶԳ��Կ�֪EP=EM��FP=FN����PE+PF+EF=ME+EF+NF=MN������ʱ��PEF���ܳ���ΪMN�ij���Ϊ��С����R��x��![]() �����������֪OR=OS=2��PR=PS=n����
�����������֪OR=OS=2��PR=PS=n����![]() =2�����x=��
=2�����x=��![]() ����ȥ����x=
����ȥ����x=![]() ����R��
����R��![]() ��
��![]() ������
������![]() �����n=1����P��2��1������N��2����1������M��x��y������
�����n=1����P��2��1������N��2����1������M��x��y������![]() =
=![]() ��
��![]() =
=![]() �����x=
�����x=![]() ��y=
��y=![]() ����M��
����M��![]() ��
��![]() ������MN=
������MN=![]() =
=![]() ������PEF���ܳ�����СֵΪ
������PEF���ܳ�����СֵΪ![]() ��
��