题目内容
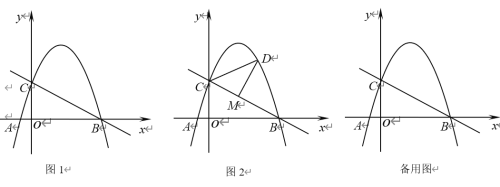
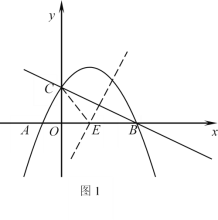
【题目】如图1,抛物线![]() 过点A(-1,0),B(4,0),与y轴相交于点C.
过点A(-1,0),B(4,0),与y轴相交于点C.
(1)求抛物线的解析式;
(2)在x轴正半轴上存在点E,使得△BCE是等腰三角形,请求出点E的坐标;
(3)如图2,点D是直线BC上方抛物线上的一个动点.过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,请求出点D的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,2或
;(3)存在,2或![]()
【解析】
(1)根据点A,B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标,结合点B的坐标可得出BC的长,设点E的坐标为(m,0),分BE=BC及CE=BE两种情况考虑:①当BE=BC时,由BE=2![]() 结合点B的坐标可得出点E的坐标;②当CE=BE时,在Rt△OCE中利用勾股定理可得出关于m的一元一次方程,解之即可得出m的值,进而可得出点E的坐标;
结合点B的坐标可得出点E的坐标;②当CE=BE时,在Rt△OCE中利用勾股定理可得出关于m的一元一次方程,解之即可得出m的值,进而可得出点E的坐标;
(3)分∠DCM=2∠ABC及∠CDM=2∠ABC两种情况考虑:①当∠DCM=2∠ABC时,取点F(0,-2),连接BF,则CD∥BF,由点B,F的坐标,利用待定系数法可求出直线BF,CD的解析式,联立直线CD及抛物线的解析式成方程组,通过解方程组可求出点D的坐标;②当∠CDM=2∠ABC时,过点C作CN⊥BF于点N,作点N关于BC的对称点P,连接NP交BC于点Q,利用待定系数法及垂直的两直线一次项系数乘积为-1可求出直线CN的解析式,联立直线BF及直线CN成方程组,通过解方程组可求出点N的坐标,利用对称的性质可求出点P的坐标,由点C、P的坐标,利用待定系数法可求出直线CP的解析式,将直线CP的解析式代入抛物线解析式中可得出关于x的一元二次方程,解之取其非零值可得出点D的横坐标.综上,此题得解.
解:(1). ∵抛物线![]() 过点
过点![]() ,
,![]() ,
,
∴![]()
解得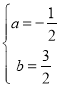
∴二次函数的表达式为:![]()
(2)抛物线![]() ,
,
当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() ;
;
∴![]() ,
,![]() ,
,![]()
∴,
![]()
![]()
①当![]() 时,如图1,
时,如图1,![]() 点是线段
点是线段![]() 的中垂线与
的中垂线与![]() 轴的交点,
轴的交点,
设![]() ,则
,则![]() ,在RT△OCE中,
,在RT△OCE中,
![]() ,解得
,解得![]() ,
,
∴![]()
②当![]() 时,
时, ![]()
∴![]()
(3)分两种情况考虑:
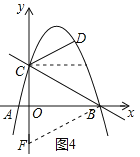
①当∠DCM=2∠ABC时,取点F(0,-2),连接BF,如图4所示.
∵OC=OF,OB⊥CF,
∴∠ABC=∠ABF,
∴∠CBF=2∠ABC.
∵∠DCB=2∠ABC,
∴∠DCB=∠CBF,
∴CD∥BF.
∵点B(4,0),F(0,-2),
∴直线BF的解析式为y=![]() x-2,
x-2,
∴直线CD的解析式为y=![]() x+2.
x+2.
联立直线CD及抛物线的解析式成方程组,得: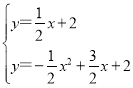 ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴点D的坐标为(2,3);
②当∠CDM=2∠ABC时,过点C作CN⊥BF于点N,作点N关于BC的对称点P,连接NP交BC于点Q,如图5所示.
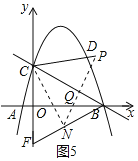
设直线CN的解析式为y=kx+c(k≠0),
∵直线BF的解析式为y=![]() x-2,CN⊥BF,
x-2,CN⊥BF,
∴k=-2.
又∵点C(0,2)在直线CN上,
∴直线CN的解析式为y=-2x+2.
连接直线BF及直线CN成方程组,得: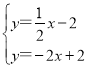 ,
,
解得: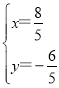 ,
,
∴点N的坐标为(![]() ).
).
∵点B(4,0),C(0,2),
∴直线BC的解析式为y=-![]() x+2.
x+2.
∵NP⊥BC,且点N(![]() ),
),
∴直线NP的解析式为y=2x-![]() .
.
联立直线BC及直线NP成方程组,得: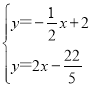 ,
,
解得: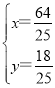 ,
,
∴点Q的坐标为(![]() ).
).
∵点N(![]() ),点N,P关于BC对称,
),点N,P关于BC对称,
∴点P的坐标为(![]() ).
).
∵点C(0,2),P(![]() ),
),
∴直线CP的解析式为y=![]() x+2.
x+2.
将y=![]() x+2代入y=-
x+2代入y=-![]() x+2整理,得:11x2-29x=0,
x+2整理,得:11x2-29x=0,
解得:x1=0(舍去),x2=![]() ,
,
∴点D的横坐标为![]() .
.
综上所述:存在点D,使得△CDM的某个角恰好等于∠ABC的2倍,点D的横坐标为2或![]() .
.

 阶梯计算系列答案
阶梯计算系列答案