题目内容
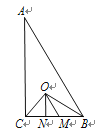
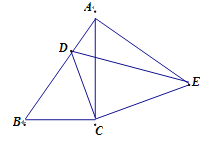
【题目】已知:如图,在四边形ABCD中,AD∥BC,M为CD中点,AM平分∠DAB,AD+BC=AB.求证:BM平分∠ABC.
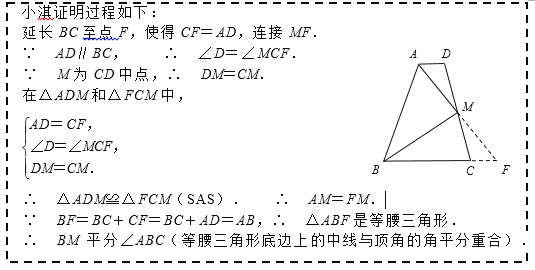
(1)请你简要叙述小淇证明方法的错误之处;
(2)若AB=5,AM=3,求四边形ABCD面积.
【答案】(1)小淇证明方法的错误之处为:并没有证明A、M、F三点共线,不能用三线合一证明BM平分∠ABC;(2)12.
【解析】
(1)小淇证明方法是:利用补短法将BC延长至F,使CF=AD,连接MF(注:此时A、M、F三点不一定共线),然后利用平行得到一组内错角相等,利用SAS证明△ADM≌△FCM,得到AM=FM再利用BF=BC+CF=BC+AD=AB证出△ABF是等腰三角形,但此时并不知道A、M、F三点是否共线,故不能用三线合一证明BM平分∠ABC.
(2)添加上证明过程A、M、F共线之后,由(1)中△ADM≌△FCM,可得S四边形ABCD=S△DAM+S四边形ABCM= S△FCM+S四边形ABCM== S△ABF,再利用勾股定理即可求出高BM,面积即可求出.
解:(1)小淇证明方法是:将BC延长至F,使CF=AD,连接MF(注:此时A、M、F三点不一定共线),然后利用AD∥BC,得到∠D=∠MCF.因为M为CD中点,所以CM=MD.利用SAS证明△ADM≌△FCM,得到AM=FM,再利用BF=BC+CF=BC+AD=AB证出△ABF是等腰三角形,但此时并不知道A、M、F三点是否共线,故不能用三线合一证明BM平分∠ABC.
(2)利用(1)的到的结论:△ADM≌△FCM
∴∠AMD=∠FMC,AM=FM,S△DAM= S△FCM
∵D、M、C三点共线,
∴∠AMD+∠AMC=180°
∴∠FMC+∠AMC=180°
∴∠AMF=180°
∴A、M、F三点共线
∵BF=BC+CF=BC+AD=AB,
∴△ABF是等腰三角形
∵AM=FM=3,
∴BM平分∠ABC,且BM⊥AC
在Rt△ABM中
BM=![]()
S四边形ABCD=S△DAM+S四边形ABCM= S△FCM+S四边形ABCM== S△ABF=![]()

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)根据计算结果填写下表:
二次项系数 | 一次项系数 | 常数项 | |
(2x + l)(x + 2) | 2 | 2 | |
(2x + 1)(3x - 2) | 6 | -2 | |
(ax + b)( mx + n) | am | bn |
(2)已知(x+ 3)2(x + mx +n)既不含二次项,也不含一次项,求m + n的值.
(3) 多项式M与多项式x2-3x + 1的乘积为2x4+ ax3 + bx2+ cx -3,则2 a +b + c的值为