题目内容
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE的度数为( ) 
A.20°
B.22.5°
C.27.5°
D.30°
【答案】B
【解析】解:∵四边形ABCD是矩形, ∴AC=BD,OA=OC,OB=OD,
∴OA=OB═OC,
∴∠OAD=∠ODA,∠OAB=∠OBA,
∴∠AOE=∠OAD+∠ODA=2∠OAD,
∵∠EAC=2∠CAD,
∴∠EAO=∠AOE,
∵AE⊥BD,
∴∠AEO=90°,
∴∠AOE=45°,
∴∠OAB=∠OBA= ![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠BAE=∠OAB﹣∠OAE=22.5°.
故选B.
【考点精析】本题主要考查了矩形的性质的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.

练习册系列答案
相关题目
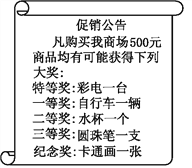
【题目】某商场进行有奖促销活动.活动规则:购买500元商品就可以获得一次转转盘的机会(转盘被分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖、纪念奖),转动转盘停止后,指针指在哪个获奖区域就可以获得该区域相应等级奖品一件(奖品设置如图所示).商场工作人员在制作转盘时,将获奖区域扇形圆心角分配如下表:
奖次 | 特等奖 | 一等奖 | 二等奖 | 三等奖 | 纪念奖 |
圆心角 | 1° | 10° | 30° | 90° | 229° |
(1)转动一次转盘,获得圆珠笔的概率是多少?
(2)如果不用转盘,请设计一种等效活动方案
(要求写清替代工具和活动规则).