题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,直线l1:y= ![]() x与直线l2:y=﹣x+6交于点A,l2与x轴交于B,与y轴交于点C.
x与直线l2:y=﹣x+6交于点A,l2与x轴交于B,与y轴交于点C.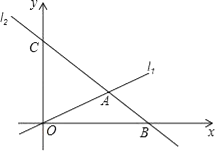
(1)求△OAC的面积;
(2)如点M在直线l2上,且使得△OAM的面积是△OAC面积的 ![]() ,求点M的坐标.
,求点M的坐标.
【答案】
(1)解:在y=﹣x+6中,令x=0,解得y=6,
∴C(0,6),即CO=6,
解方程组  ,可得
,可得 ![]() ,
,
∴A(4,2),
∴S△OAC= ![]() ×6×4=12
×6×4=12
(2)解:分两种情况:
①如图所示,
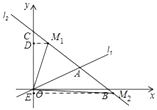
当点M1在射线AC上时,过M1作M1D⊥CO于D,则△CDM1是等腰直角三角形,
∵A(4,2),C(0,6),
∴AC= ![]() =4
=4 ![]() ,
,
∵△OAM的面积是△OAC面积的 ![]() ,
,
∴AM1= ![]() AC=3
AC=3 ![]() ,
,
∴CM1= ![]() ,
,
∴DM1= ![]() ,即点M1的横坐标为
,即点M1的横坐标为 ![]() ,
,
在直线y=﹣x+6中,当x= ![]() 时,y=6﹣
时,y=6﹣ ![]() ,
,
∴M1( ![]() ,6﹣
,6﹣ ![]() );
);
②如图所示,当点M2在射线AB上时,过M2作M2E⊥CO于E,则△CEM2是等腰直角三角形,
由题可得,AM2=AM1=3 ![]() ,
,
∴CM2=7 ![]() ,
,
∴EM2= ![]() ,即点M2的横坐标为
,即点M2的横坐标为 ![]() ,
,
在直线y=﹣x+6中,当x= ![]() 时,y=6﹣
时,y=6﹣ ![]() ,
,
∴M2( ![]() ,6﹣
,6﹣ ![]() ).
).
综上所述,点M的坐标为( ![]() ,6﹣
,6﹣ ![]() )或(
)或( ![]() ,6﹣
,6﹣ ![]() ).
).
【解析】(1)先求出两直线的交点A的坐标,及直线BC与y轴的交点C的坐标,再根据三角形的面积公式,即可求出△OAC的面积。
(2)抓住已知条件中的关键词点M在直线l2上,因此分两种情况讨论:当点M1在射线AC上时,过M1作M1D⊥CO于D,则△CDM1是等腰直角三角形,易求出AC的长,再根据△OAM和△OAC的面积关系求出AM1,CM1的长,由△CDM1是等腰直角三角形,可得出DM1的长,然后结合函数解析式就可求出 点M1的坐标;当点M2在射线AB上时,过M2作M2E⊥CO于E,则△CEM2是等腰直角三角形,运用类似的方法求出点M2的坐标,即可得出结论。
【考点精析】利用等腰直角三角形和确定一次函数的表达式对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.

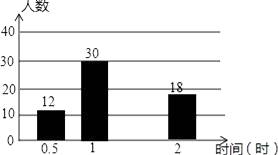
【题目】在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时) | 频数(人数) | 频率 |
0.5 | 12 | 0.12 |
1 | 30 | 0.3 |
1.5 | x | 0.4 |
2 | 18 | y |
合计 | m | 1 |
(1)统计表中的x= , y=;
(2)被调查同学劳动时间的中位数是 时;
(3)请将频数分布直方图补充完整;
(4)求所有被调查同学的平均劳动时间.