Question

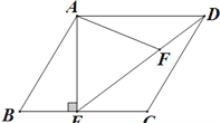
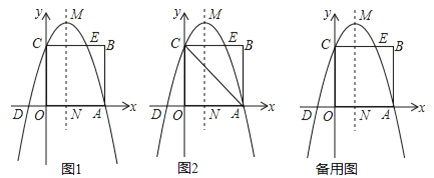
【题目】如图1，在平面直角坐标系中，正方形OABC的顶点A和C分别在x轴和y轴正半轴上，点B坐标为（3，3），抛物线y=﹣x2+bx+c过点A、C，交x轴负半轴于点D，与BC边的另一个交点为E，抛物线的顶点为M，对称轴交x轴于点N．

（1）求抛物线的函数关系式；

（2）点P在直线MN上，求当PE+PA的值最小时点P的坐标；

（3）如图2，探索在x轴是否存在一点F，使∠CFO=∠CDO﹣∠CAO？若存在，求点F的坐标；不存在，说明理由；

（4）将抛物线沿y轴方向平移m个单位后，顶点为Q，若QO平分∠CQN，求点Q的坐标．

Answer 1

【答案】（1）y=-x2+2x+3；（2）P（1，2）（3）F（6，0），（-6，0）；（4）Q（1， ），（1， ）

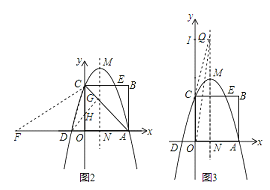
【解析】试题分析：（1）由已知条件易得点A和点C的坐标，再利用待定系数法即可求得函数的解析式；（2）AC与对称轴的交点就是P，利用待定系数法求得AC的解析式，即可求得点P的坐标；（3）在y轴的正半轴上截取OH=OD=1，则H的坐标是（0，1），延长DH交AC于点G，则DG⊥AC，∠CDH=∠CDO﹣∠CAO，当F在x轴的负半轴上时，当∠CFO=∠CDH=∠CDO﹣∠CAO时，则△CFO∽△CDG，根据相似三角形的对应边的比相等即可求得OF的长，则F的坐标即可求得，然后根据对称性求得F在x轴的正半轴时的坐标；

（4）当抛物线沿y轴的正半轴移动时，Q的横坐标是1，QO平分∠CQN，则CQ=OC，利用勾股定理即可求得Q的纵坐标；同理求得抛物线沿y轴的负半轴移动时Q的坐标．

试题解析： 解：（1）∵四边形OABC是正方形，B的坐标是（3，3），

∴A的坐标是（3，0），C的坐标是（0，3）．

根据题意得，

解得：，

则二次函数的解析式是y=﹣x2+2x+3；

（2）设直线AC的解析式是y=ax+b，

，

解得：，

则直线AC的解析式是y=﹣x+3，

当x=1时，y=﹣1+3=2，

则P的坐标是（1，2）；

（3）在y=﹣x2+2x+3中令y=0，则﹣x2+2x+3=0，解得x=﹣1或x=3．

则D的坐标是（﹣1，0）A的坐标是（3，0）．

在y轴的正半轴上截取OH=OD=1，则H的坐标是（0，1），延长DH交AC于点G，则DG⊥AC；

∵直角△ODF中，OH=OD，

∴∠HDO=45°，

同理，∠CAO=45°，

∴∠HDO=∠CAO．则∠CDH=∠CDO﹣∠CAO．

当F在x轴的负半轴上时，

设DG的解析式是y=ex+f，则，

解得，则DG的解析式是y=x+1．

根据题意得：，

解得：，

则G的坐标是（1，2）．

则DG=，CD=，CG=．

当∠CFO=∠CDH=∠CDO﹣∠CAO时，△CFO∽△CDG，

则，即，解得：OF=6，

则F的坐标是（﹣6，0）．

根据对称性可得当F在x轴的正半轴上时F的坐标是（6，0）；

（4）当抛物线沿y轴的正半轴移动时，如图3，

设Q的坐标是（1，n）．作QI⊥y轴于点I．则IQ=1，IC=n﹣3，

则QO平分∠CQN，则CQ=OC=3，12+（n﹣3）2=32，

解得：n=3+2，

则Q的坐标是（1，3+2）；

同理，当抛物线沿y轴的负方向移动时Q的坐标是（1，3﹣2）．

总之，Q的坐标是（1，3+2）或（1，3﹣2）．