题目内容
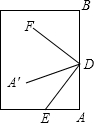如图，文文把一张长方形的纸沿着DE、DF折了两次，使A、B都落在DA′上，则∠EDF的度数为90°
90°
．分析：根据折叠的性质可得：∠BDF=∠A′DF，∠ADE=∠A′DE，又由平角的定义可得：∠BDF+∠A′DF+∠ADE+∠A′DE=180°，则可求得∠EDF的度数．
解答：解：∵把一张长方形的纸沿着DE、DF折了两次，使A、B都落在DA′上，
∴根据折叠的性质可得：∠BDF=∠A′DF，∠ADE=∠A′DE，
∵∠BDF+∠A′DF+∠ADE+∠A′DE=180°，
∴2∠A′DF+2∠A′DE=180°，
∴∠A′DF+∠A′DE=90°，
即∠EDF=90°．
故答案为：90°．
∴根据折叠的性质可得：∠BDF=∠A′DF，∠ADE=∠A′DE，
∵∠BDF+∠A′DF+∠ADE+∠A′DE=180°，
∴2∠A′DF+2∠A′DE=180°，
∴∠A′DF+∠A′DE=90°，
即∠EDF=90°．
故答案为：90°．
点评：此题考查了折叠的性质．此题比较简单，解题的关键是掌握折叠的性质，注意折叠前后图形是全等的，注意折叠中的对应关系．
练习册系列答案
名校课堂系列答案
相关题目
长为
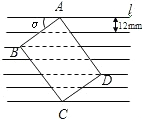
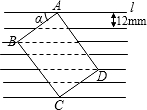如图所示，把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中，恰好四个顶点都在横格线上，已知α=36°，求长方形卡片的周长．（精确到1mm）（参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）
18、（经典题）如图所示，把一张长方形纸片ABCD沿EF折叠后，点C，D分别落在C′，D′的位置上，EC′交AD于点G，已知∠EFG=58°，求∠BEG度数．
（2011•同安区模拟）如图，小明把一张矩形的硬纸板ABCD的四周各剪去一个边长为x（cm）的小正方形，再折合成一个无盖的长方体盒子，已知：AB=12cm，AD=10cm．请填写下表