题目内容
小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知α=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)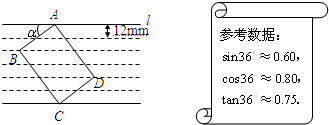
分析:求ABCD的周长就是求AB和AD的长,可分别过B、D作垂线垂直于l,通过构造直角三角形根据α=36°和ABCD的四个顶点恰好在横格线且每个横格宽12mm等条件来求出AB、AD的长.
解答: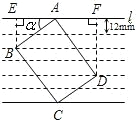 解:作BE⊥l于点E,DF⊥l于点F.
解:作BE⊥l于点E,DF⊥l于点F.
∵α+∠DAF=180°-∠BAD=180°-90°=90°,
∠ADF+∠DAF=90°,
∴∠ADF=α=36°.
根据题意,得BE=24mm,DF=48mm.
在Rt△ABE中,sinα=
,
∴AB=
=
=40(mm).
在Rt△ADF中,cos∠ADF=
,
∴AD=
=
=60(mm).
∴矩形ABCD的周长=2(40+60)=200(mm).
 解:作BE⊥l于点E,DF⊥l于点F.
解:作BE⊥l于点E,DF⊥l于点F.∵α+∠DAF=180°-∠BAD=180°-90°=90°,
∠ADF+∠DAF=90°,
∴∠ADF=α=36°.
根据题意,得BE=24mm,DF=48mm.
在Rt△ABE中,sinα=
| BE |
| AB |
∴AB=
| BE |
| sin36° |
| 24 |
| 0.60 |
在Rt△ADF中,cos∠ADF=
| DF |
| AD |
∴AD=
| DF |
| cos36° |
| 48 |
| 0.80 |
∴矩形ABCD的周长=2(40+60)=200(mm).
点评:通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中解决.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
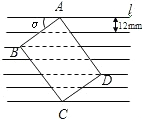 长为
长为 放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知
放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知 =36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
 放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知
放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知 =36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
