题目内容
（2004•泉州）如图，AD是直角三角形△ABC斜边上的中线，把ADC沿AD对折，点C落在点C′处，连接CC′，则图中共有等腰三角形 个．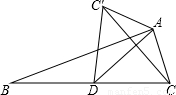
【答案】分析：经过翻折变换的图形与原图形全等，及等腰三角形的判定得出．
解答：解：∵AD是直角三角形△ABC斜边上的中线，
∴AD=BD=CD，△ABD，△ACD是等腰三角形．
∵△ADC′是△ADC翻折变换后的图形，
∴AC′=AC，CD=C′D，故△ACC′，与△CDC′是等腰三角形．
∵AD=CD，CD=C′D，
∴△ADC′是等腰三角形．
故图中共有等腰三角形5个．
点评：本题很简单，解答此题的关键是熟知经过翻折变换的图形与原图形全等．
解答：解：∵AD是直角三角形△ABC斜边上的中线，
∴AD=BD=CD，△ABD，△ACD是等腰三角形．
∵△ADC′是△ADC翻折变换后的图形，
∴AC′=AC，CD=C′D，故△ACC′，与△CDC′是等腰三角形．
∵AD=CD，CD=C′D，
∴△ADC′是等腰三角形．
故图中共有等腰三角形5个．
点评：本题很简单，解答此题的关键是熟知经过翻折变换的图形与原图形全等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
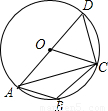
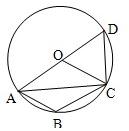（2004•泉州）如图，⊙O为四边形ABCD的外接圆，圆心O在AD上，OC∥AB．
