题目内容
已知二次函y=x2-2x-3的图象x轴交于A、B两点,点C是抛物线上异于A、B的一个点,△ABC的面积等于分析:由题知有且只有三个c点,说明有三个三角形面积相等,因为底AB已经定了,只要高相等就行,于是有一个点c在抛物线顶点上,则问题就解决了.
解答:解:因为y=x2-2x-3=(x-3)×(x+1),
则有A(-1,0),B(3,0)即AB=4
∵顶点横坐标x=-
=1代入y=x2-2x-3得顶点(1,-4)
∴s=
×AB×4=8.
则有A(-1,0),B(3,0)即AB=4
∵顶点横坐标x=-
| b |
| 2a |
∴s=
| 1 |
| 2 |
点评:考查二次函数的性质和数形结合,属于大众型题目,相对容易.

练习册系列答案
相关题目
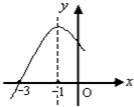 10、已知二次函y=-x2-2x+m的部分图象如图所示,则关于l的一元二次方程-x2-2x+m=0的解为
10、已知二次函y=-x2-2x+m的部分图象如图所示,则关于l的一元二次方程-x2-2x+m=0的解为