题目内容
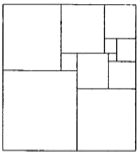
【题目】图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。
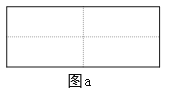

(1)你认为图b中的阴影部分的正方形的边长等于__________________。
(2)请用两种不同的方法求图b中阴影部分的面积。
方法1:___________________________ 方法2:___________________________
(3)观察图b,你能写出下列三个代数式之间的等量关系吗?
代数式: (m+n)2 ,(m-n)2,mn
_______________________________________________________
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,求(a-b)2的值。
【答案】(1)m-n;(2)方法1:(m-n)2;方法2:(m+n)2 –4mn;(3)(m+n)2 -4mn=(m-n)2;(4)29.
【解析】
(1)根据阴影部分的正方形的边长等于小长方形的长减去宽即可求解;(2)根据阴影部分的面积为小正方形的面积和阴影部分的面积等于边长为m+n的正方形的面积减去4个长为m,宽为n的长方形的面积两种表示法求解即可;(3)观察图形,结合(2)的结果即可解答;(4)利用(3)中的结论即可解答.
(1)m-n;
(2)方法1:(m-n)2;方法2:(m+n)2 –4mn;
(3)(m+n)2 -4mn=(m-n)2;
(4)(a-b)2=(a+b)2-4ab=49-20=29.

 阅读快车系列答案
阅读快车系列答案【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?