题目内容
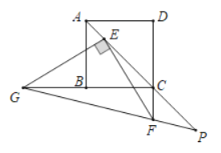
【题目】如图,正方形ABCD的对角线AC上有一点E,且CE=4AE,点F在DC的延长线上,连接EF,过点E作EG⊥EF,交CB的延长线于点G,连接GF并延长,交AC的延长线于点P,若AB=5,CF=2,则线段EP的长是_____.
【答案】![]()
【解析】
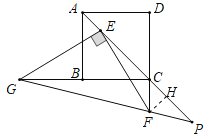
如图,作FH⊥PE于H.利用勾股定理求出EF,再证明△CEF∽△FEP,可得EF2=ECEP,由此即可解决问题.
如图,作FH⊥PE于H.
∵四边形ABCD是正方形,AB=5,
∴AC=5![]() ,∠ACD=∠FCH=45°,
,∠ACD=∠FCH=45°,
∵∠FHC=90°,CF=2,
∴CH=HF=![]() ,
,
∵CE=4AE,
∴EC=4![]() ,AE=
,AE=![]() ,
,
∴EH=5![]() ,
,
在Rt△EFH中,EF2=EH2+FH2=(5![]() )2+(
)2+(![]() )2=52,
)2=52,
∵∠GEF=∠GCF=90°,
∴E,G,F,C四点共圆,
∴∠EFG=∠ECG=45°,
∴∠ECF=∠EFP=135°,
∵∠CEF=∠FEP,
∴△CEF∽△FEP,
∴![]() ,
,
∴EF2=ECEP,
∴EP=![]()
故答案为:![]() .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
【题目】甲、乙两个工程队需完成A、B两个工地的工程.若甲、乙两个工程队分别可提供40个和50个标准工作量,完成A、B两个工地的工程分别需要70个和20个标准工作量,且两个工程队在A、B两个工地的1个标准工作量的成本如下表所示:
A工地 | B工地 | |
甲工程队 | 800元 | 750元 |
乙工程队 | 600元 | 570元 |
设甲工程队在A工地投入x(20≤x≤40)个标准工作量,完成这两个工程共需成本y元.
(1)求y与x之间的函数关系式;
(2)请判断y是否能等于62000,并说明理由.