题目内容
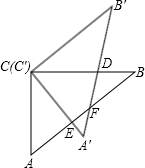 (易错题)如图,△ABC和△A′B′C′中,AC=A′C′=3,BC=B′C′=4,AB=A′B′=5,将顶点C′与C重合,△A′B′C′绕着点C旋转,旋转过程中,A′C′交AB于点E,A′B′交AB于点F,交BC于点D.
(易错题)如图,△ABC和△A′B′C′中,AC=A′C′=3,BC=B′C′=4,AB=A′B′=5,将顶点C′与C重合,△A′B′C′绕着点C旋转,旋转过程中,A′C′交AB于点E,A′B′交AB于点F,交BC于点D.(1)当A′C′⊥AB时,判断△C′DB′和△A′C′D的形状;
(2)当△ACE为等腰三角形时,求出此时AE的值.
分析:(1)首先运用勾股定理的逆定理证明△ABC,△A'B'C'都是直角三角形,然后证明当A′C′⊥AB时,∠ACE=∠B,而由∠B=∠B',得出∠BCB'=∠B',从而证明△C′DB′是等腰三角形.同理得出△A′C′D也是等腰三角形.
(2)当△ACE为等腰三角形时,有三种可能:AE=AC;AE=EC;AC=CE.需要分类求解.
(2)当△ACE为等腰三角形时,有三种可能:AE=AC;AE=EC;AC=CE.需要分类求解.
解答:解:(1)∵32+42=52,
∴△ABC,△A′B′C′都是直角三角形,且△ABC≌△A′B′C′.
∴∠B=∠B′.
当A′C′⊥AB时,由旋转可知∠ACE=∠B′CB,
由互余关系可得∠ACE=∠B,
∴∠BCB'=∠B′,
∴∠BCB'=∠B,
∴△C′DB′是等腰三角形.
同理得△A′C′D也是等腰三角形.
(2)△ACE为等腰三角形,有三种可能.
①当AE=AC时,AE=AC=3;
②当AE=EC时,E点为线段AB的中点,AE=
AB=2.5;
③当AC=CE时,过C点作AB边上的高CM.
由面积法得CM•AB=AC•BC,
∴CM=2.4,
∴AM=
=1.8,
∴AE=2AM=3.6.
故AE=3或2.5或3.6.
∴△ABC,△A′B′C′都是直角三角形,且△ABC≌△A′B′C′.
∴∠B=∠B′.
当A′C′⊥AB时,由旋转可知∠ACE=∠B′CB,
由互余关系可得∠ACE=∠B,
∴∠BCB'=∠B′,
∴∠BCB'=∠B,
∴△C′DB′是等腰三角形.
同理得△A′C′D也是等腰三角形.
(2)△ACE为等腰三角形,有三种可能.

①当AE=AC时,AE=AC=3;
②当AE=EC时,E点为线段AB的中点,AE=
| 1 |
| 2 |
③当AC=CE时,过C点作AB边上的高CM.
由面积法得CM•AB=AC•BC,
∴CM=2.4,
∴AM=
| AC2-CM2 |
∴AE=2AM=3.6.
故AE=3或2.5或3.6.
点评:本题主要考查旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要学会运用勾股定理解决直角三角形中的线段问题.

练习册系列答案
相关题目
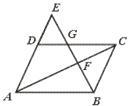 6、(易错题)如图,?ABCD中,E是AD延长线上一点,BE交AC于点F,交DC于点G,则下列结论中错误的是( )
6、(易错题)如图,?ABCD中,E是AD延长线上一点,BE交AC于点F,交DC于点G,则下列结论中错误的是( )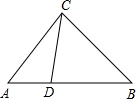 (易错题)如图∠CAB=∠BCD,AD=2,BD=4,则BC=
(易错题)如图∠CAB=∠BCD,AD=2,BD=4,则BC=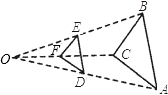 们的中点D、E、F,得△DEF,下列说法正确的个数是( )
们的中点D、E、F,得△DEF,下列说法正确的个数是( )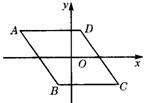 5、(易错题)如图,菱形ABCD的中心在直角坐标系的坐标原点上,且AD∥x轴,点A的坐标为(-4,2),点D的横坐标是1,则点B的坐标为
5、(易错题)如图,菱形ABCD的中心在直角坐标系的坐标原点上,且AD∥x轴,点A的坐标为(-4,2),点D的横坐标是1,则点B的坐标为