Question

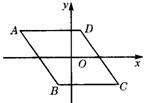5、（易错题）如图，菱形ABCD的中心在直角坐标系的坐标原点上，且AD∥x轴，点A的坐标为（-4，2），点D的横坐标是1，则点B的坐标为

（-1，-2）

，点C的坐标为

（4，-2）

，点D的坐标为

（1，2）

．

Answer 1

分析：菱形四边相等，本题可从菱形ABCD的中心在直角坐标系的坐标原点上入手得知A、C关于原点对称，进而得出C点的坐标．根据BC∥x轴可知B点的纵坐标，再根据中心对称可知D点的坐标．

解答：解：菱形ABCD的中心在直角坐标系的坐标原点上，因而A、C关于原点对称，因而点C的坐标是（4，-2）；
BC∥x轴因而B的纵坐标是-2，同理D点的纵坐标是2，因而点B的坐标为（-1，-2），点C的坐标为（4，-2），
点D的坐标为（1，2）．
故答案为（-1，-2），（4，-2），（1，2）．

点评：本题综合考查了图形的性质和坐标的确定，是综合性较强，难度较大的综合题．