题目内容
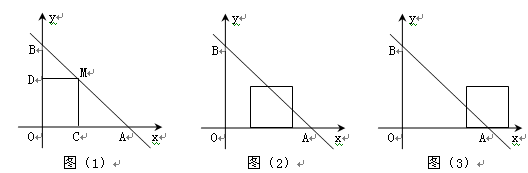
(9分)如图,直线 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
 |
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为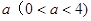 ,正方形OCMD与△AOB重叠部分的面积为S.试求S与
,正方形OCMD与△AOB重叠部分的面积为S.试求S与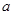 的函数关系式并画出该函数的图象.
的函数关系式并画出该函数的图象.
(1)设点M的横坐标为x,则点M的纵坐标为-x+4(0<x<4,x>0,-x+4>0);
则:MC=∣-x+4∣=-x+4,MD=∣x∣=x;
∴C四边形OCMD=2(MC+MD)=2(-x+4+x)=8
∴当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8;
…………3分
(2)根据题意得:S四边形OCMD=MC·MD=(-x+4)· x
=-x2+4x=-(x-2)2+4
∴四边形OCMD的面积是关于点M的横坐标x(0<x<4)的二次函数,并且当x=2,即当点M运动到线段AB的中点时,四边形OCMD的面积最大且最大面积为4;
…………………6分
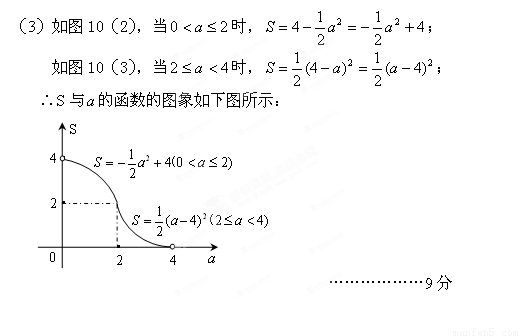
【解析】略

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案(9分)如图,直线![]() 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
 |
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为![]() ,正方形OCMD与△AOB重叠部分的面积为S.试求S与
,正方形OCMD与△AOB重叠部分的面积为S.试求S与![]() 的函数关系式并画出该函数的图象.
的函数关系式并画出该函数的图象.
(9分)如图,直线 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
 |
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为
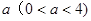 ,正方形OCMD与△AOB重叠部分的面积为S.试求S与
,正方形OCMD与△AOB重叠部分的面积为S.试求S与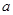 的函数关系式并画出该函数的图象.
的函数关系式并画出该函数的图象.  已知:如图,直线与两坐标轴相交于A、B两点,
已知:如图,直线与两坐标轴相交于A、B两点,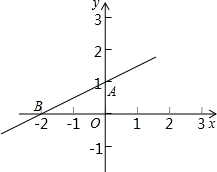 已知:如图,直线与两坐标轴相交于A、B两点,
已知:如图,直线与两坐标轴相交于A、B两点,