题目内容
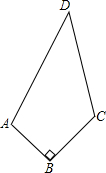如图，凸四边形ABCD的四边AB、BC、CD、和DA的长分别是3，4，12，和13，∠ABC=90°，则四边形
ABCD的面积S=________．
36
分析：连接AC，在直角△ABC中，已知AB、BC根据勾股定理可以求得AC=5，在△ACD中，AC2+CD2=AD2，根据勾股定理的逆定理确定△ADC为直角三角形，四边形ABCD的面积为△ACD和△ABC面积之和．
解答：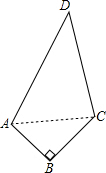
解：连接AC，
在直角△ABC中，AB=3，BC=4，则AC=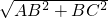
=5，
又∵AC2+CD2=AD2，∴△ACD为直角三角形，
∴Rt△ABC的面积为
×3×4=6，
Rt△ACD的面积为×5×12=30，
∴四边形ABCD的面积为△ACD和△ABC面积之和，
S=30+6=36．
故答案为 36．
点评：本题考查了勾股定理在直角三角形中的运用，考查了直角三角形面积的计算，本题中判定△ACD为直角三角形是解题的关键．
分析：连接AC，在直角△ABC中，已知AB、BC根据勾股定理可以求得AC=5，在△ACD中，AC2+CD2=AD2，根据勾股定理的逆定理确定△ADC为直角三角形，四边形ABCD的面积为△ACD和△ABC面积之和．
解答：
解：连接AC，在直角△ABC中，AB=3，BC=4，则AC=
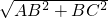=5，又∵AC2+CD2=AD2，∴△ACD为直角三角形，
∴Rt△ABC的面积为
×3×4=6，Rt△ACD的面积为
×5×12=30，∴四边形ABCD的面积为△ACD和△ABC面积之和，
S=30+6=36．
故答案为 36．
点评：本题考查了勾股定理在直角三角形中的运用，考查了直角三角形面积的计算，本题中判定△ACD为直角三角形是解题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
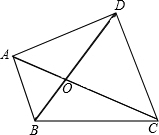已知凸四边形ABCD的对角线AC，BD相交于点O，且△ABC，△ACD，△ABD的面积分别为S1=5，S2=10，S3=6．求△ABO的面积（如图）．
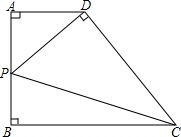如图，在凸四边形ABCD中，AB的长为2，P是边AB的中点，若∠DAB=∠ABC=∠PDC=90°，则四边形ABCD的面积的最小值是（ ）
A、C两点分别在x轴、y轴上．将△ABC沿AC翻折，点B落到B′处，B′C交x轴于点D，且sin∠OCD=