题目内容
【题目】已知:二次函数![]() 与
与![]() 轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程![]() 的两个根.
的两个根.
(1)请直接写出点A、B的坐标,并求出该二次函数的解析式.
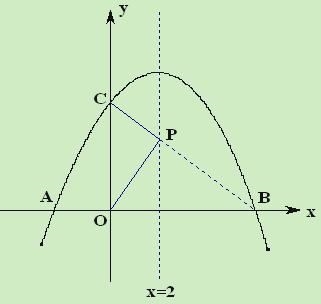
(2)如图1,在二次函数对称轴上是否存在点P,使![]() 的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合). 过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当![]() 面积S最大时,求m的值.
面积S最大时,求m的值.

【答案】(1)A(-2,0)、B(6,0)
(2)将A(-2,0)、B(6,0)代入![]() 则
则![]()
∴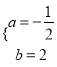
则![]()
∴对称轴为直线![]() 顶点为
顶点为![]()
(3)∵A、B两点关于对称轴![]() 对称,连结BC交对称轴
对称,连结BC交对称轴![]() 于点P,则点P即为所求
于点P,则点P即为所求
∵B(6,0)、C(0,6) 所以过BC两点的直线为: ![]()
将![]() 代入,则
代入,则![]() ∴ P(2,4)
∴ P(2,4)
(4)∵Q(m,0) 0<m<6 ∴ AQ="2+m " BQ=6-m
![]()
![]() QD∥AC,
QD∥AC, ![]() ∽
∽![]()
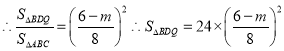
![]()
∴当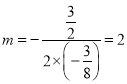 时,
时, ![]() 的面积最大. 即 m=2
的面积最大. 即 m=2
【解析】试题分析:(1)、根据方程求出求出A、B两点的坐标,将A、B两点坐标代入解析式求出解析式;(2)、根据轴对称的性质作出点P,然后求出直线BC的解析式,得出点P的坐标;(3)、根据题意得出AQ和BQ的长度,然后求出△ACQ和△ABC的面积,根据三角形相似得出△BDQ与m之间的函数关系式,根据二次函数的性质求出最值.
试题解析:(1)、A(-2,0)、B(6,0),将A(-2,![]() 则
则![]() ∴
∴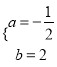 则
则![]()
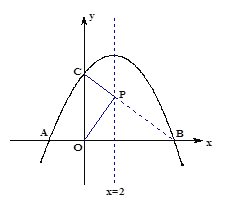
(2)、∵A、B两点关于对称轴![]() 对称,连结BC交对称轴
对称,连结BC交对称轴![]() 于点P,则点P即为所求.
于点P,则点P即为所求.
∵B(6,0)、C(0,6) 所以过BC两点的直线为: ![]()
将![]() 代入,则
代入,则![]() ∴ P(2,4)
∴ P(2,4)
(3)、∵Q(m,0) 0<m<6 ∴ AQ=2+m BQ=6-m
![]()
![]() QD∥AC,
QD∥AC, ![]() ∽
∽![]()
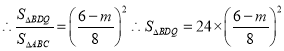
![]()
∴当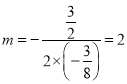 时,
时, ![]() 的面积最大. 即 m=2 .
的面积最大. 即 m=2 .