题目内容
如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=
,求AD的长.

(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=
| 4 |
| 5 |

(1)AC与⊙O相切.
证明:∵弧BD是∠BED与∠BAD所对的弧,
∴∠BAD=∠BED,
∵OC⊥AD,
∴∠AOC+∠BAD=90°,
∴∠BED+∠AOC=90°,
即∠C+∠AOC=90°,
∴∠OAC=90°,
∴AB⊥AC,即AC与⊙O相切;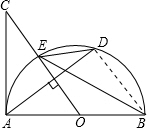
(2)连接BD.
∵AB是⊙O直径,
∴∠ADB=90°,
在Rt△AOC中,∠CAO=90°,
∵AC=8,∠ADB=90°,cos∠C=cos∠BED=
,
∴AO=6,
∴AB=12,
在Rt△ABD中,∵cos∠OAD=cos∠BED=
,
∴AD=AB•cos∠OAD=12×
=
.
证明:∵弧BD是∠BED与∠BAD所对的弧,
∴∠BAD=∠BED,
∵OC⊥AD,
∴∠AOC+∠BAD=90°,
∴∠BED+∠AOC=90°,
即∠C+∠AOC=90°,
∴∠OAC=90°,
∴AB⊥AC,即AC与⊙O相切;

(2)连接BD.
∵AB是⊙O直径,
∴∠ADB=90°,
在Rt△AOC中,∠CAO=90°,
∵AC=8,∠ADB=90°,cos∠C=cos∠BED=
| 4 |
| 5 |
∴AO=6,
∴AB=12,
在Rt△ABD中,∵cos∠OAD=cos∠BED=
| 4 |
| 5 |
∴AD=AB•cos∠OAD=12×
| 4 |
| 5 |
| 48 |
| 5 |

练习册系列答案
相关题目
 切线AM上一点(D与A不重合),DE切⊙O于点E,与BN交于点C,且AD<BC.设AD=m,BC=n.
切线AM上一点(D与A不重合),DE切⊙O于点E,与BN交于点C,且AD<BC.设AD=m,BC=n.





