Question

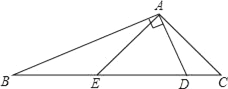
【题目】如图．△ABC中，∠C=2∠B，D是BC上一点，且AD⊥AB，点E是BD的中点，连结AE．

（1）求证：BD=2AC；

（2）若AE=6.5，AD=5，那么△ABE的周长是多少？

Answer 1

【答案】（1）见解析；（2）25

【解析】

（1）在Rt△ADB中，点E是BD的中点；根据直角三角形的性质，可得BE=AE，故∠AEC=2∠B=∠C；AE=AC，代换可得结论；
（2）根据勾股定理可得AB的长，结合（1）的结论，可得答案．

（1）证明：∵AD⊥AB，

∴∠BAD=90°，又点E是BD的中点，

∴

∴∠EAB=∠EBA，

∴∠AEC=2∠B，又∠C=2∠B，

∴∠AEC=∠C，

∴AE=AC，

∴BD=2AC；

（2）解：∵∠BAD=90°，点E是BD的中点，

∴BD=2AE=13，EA=EB=6.5，

由勾股定理得，

∴△ABE的周长=AB+AE+BE=12+6.5+6.5=25．