题目内容
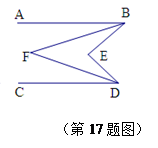
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
∠1=∠2,且∠3=115°,求∠ACB的度数.
∠1=∠2,且∠3=115°,求∠ACB的度数.

∵CD⊥AB, EF⊥AB ∴∠BFE=∠BDC=90°
∴CD∥EF ∴∠2=∠BCD
∵∠1=∠2 ∴∠1=∠BCD
∴DG∥BC ∴∠3=∠ACB
∵∠3=115° ∴∠ACB=115°
∴CD∥EF ∴∠2=∠BCD
∵∠1=∠2 ∴∠1=∠BCD
∴DG∥BC ∴∠3=∠ACB
∵∠3=115° ∴∠ACB=115°
先根据已知条件判断出DG∥BC,再根据两直线平行,同位角相等即可得出结论.【题型】解答题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 交两条平行线
交两条平行线 于点
于点 , 若
, 若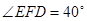 , 则图中等于
, 则图中等于 的角的个数是
的角的个数是