Question

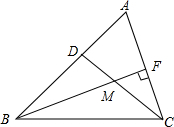
如图，在△ABC中，CD平分∠ACB，BF是△ABC的高，BF、CD相交于点M．
（1）若∠A=80°，∠ABC=50°，求∠BMC的度数．
（2）若其他条件均不变，只把题中的“BF是△ABC的高”改为“BF是△ABC的角平分线”的情况下，请探索∠A与∠BMC的数量关系，并说明理由．

Answer 1

（1）∵∠A=80°，∠ABC=50°，
∴∠ACB=180°-∠A-∠ABC=180°-80°-50°=50°，
∵CD平分∠ACB，
∴∠ACD=

1

2

∠ACB=

1

2

×50°=25°，
∵BF是△ABC的高，
∴∠CFM=90°，
∴∠BMC=∠ACD+∠CFM=25°+90°=115°；

（2）∠BMC=90°+

1

2

∠A．
理由如下：在△ABC中，∠ABC+∠ACB=180°-∠A，
∵BF、CD是△ABC的角平分线，
∴∠MBC=

1

2

∠ABC，∠MCB=

1

2

∠ACB，
∴∠MBC+∠MCB=

1

2

（∠ABC+∠ACB）=

1

2

（180°-∠A），
在△BMC中，∠BMC=180°-（∠MBC+∠MCB）=180°-

1

2

（180°-∠A）=90°+

1

2

∠A，
即∠BMC=90°+

1

2

∠A．