题目内容
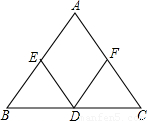
在等腰△ABC的底边BC上任取一点D,作DE∥AC、DF∥AB,分别交AB、AC于点E、F,若等腰△ABC的腰长为m,底边长为n,则四边形AEDF的周长为( )
A、2m B、2n C、m+n D、2m-n
【答案】
A
【解析】
试题分析:根据等腰三角形和平行四边形的性质,可推出DF=CF、BE=DE,从而将四边形AEDF的周长转化到等腰△ABC的腰上求解.

∵AB=AC,
∴∠B=∠C,
∵DF∥AB,
∴∠B=∠FDC,
∴∠FDC=∠C,
∴DF=FC,
同理DE=BE,
∵DF∥AB,DE∥AC,
∴四边形AEDF是平行四边形,
∴▱AEDF的周长=AE+DE+DF+AF=AE+BE+AF+CF=AB+AC=2AC=2m,
故选A.
考点:本题考查了三角形的中位线定理,等腰三角形的性质
点评:解答本题的关键是熟练掌握三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
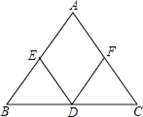
 14、如图,在等腰△ABC的底边BC上任取一点D,作DE∥AC、DF∥AB,分别交AB、AC于点E、F,若等腰△ABC的腰长为m,底边长为n,则四边形AEDF的周长为( )
14、如图,在等腰△ABC的底边BC上任取一点D,作DE∥AC、DF∥AB,分别交AB、AC于点E、F,若等腰△ABC的腰长为m,底边长为n,则四边形AEDF的周长为( )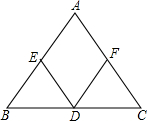 如图,在等腰△ABC的底边BC上任取一点D,作DE∥AC、DF∥AB,分别交AB、AC于点E、F,若等腰△ABC的腰长为m,底边长为n,则四边形AEDF的周长为
如图,在等腰△ABC的底边BC上任取一点D,作DE∥AC、DF∥AB,分别交AB、AC于点E、F,若等腰△ABC的腰长为m,底边长为n,则四边形AEDF的周长为