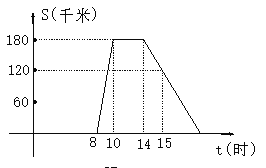
题目内容
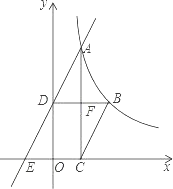
【题目】如图,已知函数y=![]() (x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(1)若AC=![]() OD,求a、b的值;
OD,求a、b的值;
(2)若BC∥AE,求BC的长.
【答案】(10![]() ,b=2;(2)
,b=2;(2) ![]() .
.
【解析】
试题分析:(1)首先利用反比例函数图象上点的坐标性质得出k的值,再得出A、D点坐标,进而求出a,b的值;
(2)设A点的坐标为:(m,![]() ),则C点的坐标为:(m,0),得出tan∠ADF=
),则C点的坐标为:(m,0),得出tan∠ADF= ,tan∠AEC=
,tan∠AEC= ,进而求出m的值,即可得出答案.
,进而求出m的值,即可得出答案.
试题解析:(1)∵点B(2,2)在函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=4,则y=![]() ,
,
∵BD⊥y轴,∴D点的坐标为:(0,2),OD=2,
∵AC⊥x轴,AC=![]() OD,∴AC=3,即A点的纵坐标为:3,
OD,∴AC=3,即A点的纵坐标为:3,
∵点A在y=![]() 的图象上,∴A点的坐标为:(
的图象上,∴A点的坐标为:(![]() ,3),
,3),
∵一次函数y=ax+b的图象经过点A、D,
∴ ,
,
解得:![]() ,b=2;
,b=2;
(2)设A点的坐标为:(m,![]() ),则C点的坐标为:(m,0),
),则C点的坐标为:(m,0),
∵BD∥CE,且BC∥DE,
∴四边形BCED为平行四边形,
∴CE=BD=2,
∵BD∥CE,∴∠ADF=∠AEC,
∴在Rt△AFD中,tan∠ADF= ,
,
在Rt△ACE中,tan∠AEC= ,
,
∴![]() =
=![]() ,
,
解得:m=1,
∴C点的坐标为:(1,0),则BC=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目