题目内容
【题目】(阅读理解)
截长补短法,是初中数学儿何题中一种输助线的添加方法,截长就是在长边上载取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
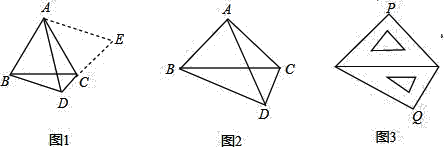
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD.连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是___________
(拓展延伸)
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
(知识应用)
(3)如图3,一副三角尺斜边长都为14cm,把斜边重叠摆放在一起,则两块三角尺的直角项点之间的距离PQ的长为________cm.
【答案】(1)![]() ;(2)
;(2)![]() ,理由见详解;(3)
,理由见详解;(3)![]() .
.
【解析】
(1)由等边三角形知![]() ,结合
,结合![]() 知
知![]() ,则
,则![]() 证得
证得![]() 得
得![]() ,再证明三角形ADE是等边三角形,等量代换可得结论;
,再证明三角形ADE是等边三角形,等量代换可得结论;
(2) 同理可证![]() 得
得![]() ,由勾股定理得
,由勾股定理得![]() ,等量代换即得结论;
,等量代换即得结论;
(3)由直角三角形的性质可得QN的长,由勾股定理可得MQ的长,由(2)知![]() ,由此可求得PQ长.
,由此可求得PQ长.
解:(1)延长DC到点E,使CE=BD.连接AE,
![]() 是等边三角形
是等边三角形
![]()
![]()
![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 是等边三角形
是等边三角形
![]()
(2)![]()
延长DC到点E,使CE=BD.连接AE,

![]() ,
,![]()
![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)连接PQ,

![]()
![]()
根据勾股定理得![]()
由(2)知![]()
![]()

 计算高手系列答案
计算高手系列答案【题目】九年级(3)班数学兴趣小组经过市场调查,整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天的销 售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x之间的函数表达式;
(2)销售该商品在第几天时,当天获得的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.