题目内容
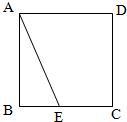22、如图，正方形纸片ABCD的边BC上有一点E，AE=8cm，若把纸片对折，使点A与点E重合，则纸片折痕的长是多少？分析：设折痕是GH，则GH是AE的中垂线，可以证明△ABE≌△HGF（SAS）得出折痕与AE相等．
解答：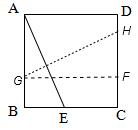
解：设G是折痕与AB的交点，H是折痕与CD的交点．
过G作GF⊥CD于F，则GF=AB，GF⊥AB．
∵正方形纸片ABCD，∴∠DFG=∠B=∠AGF=90°．
∴∠AGH+∠HGF=∠HGF+∠GHF．
∴△ABE≌△HGF．（ASA）
∴GH=AE=8．
解：设G是折痕与AB的交点，H是折痕与CD的交点．过G作GF⊥CD于F，则GF=AB，GF⊥AB．
∵正方形纸片ABCD，∴∠DFG=∠B=∠AGF=90°．
∴∠AGH+∠HGF=∠HGF+∠GHF．
∴△ABE≌△HGF．（ASA）
∴GH=AE=8．
点评：本题考查图形的折叠，同时考查了三角形全等的判断和性质、正方形的性质等几何基本知识．
练习册系列答案
阅读快车系列答案
相关题目
（2013•昆山市二模）如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，则EF的长为
（2012•宽城区一模）如图，正方形纸片ABCD，对角线AC、BD交于点O，折叠纸片，使AD落在BD上，点A恰好与BD上的点F重合，展开纸片后，折痕DE分别交AB、AC于点E、G，则∠AGD的度数为
已知：如图，正方形纸片ABCD的边长是4，点M、N分别在两边AB和CD上（其中点N不与点C重合），沿直线MN折叠该纸片，点B恰好落在AD边上点E处．