题目内容
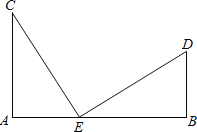
【题目】如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,
(1)△AEC≌△BDE吗,请说明理由
(2)试猜想线段CE与DE大小与位置关系,说明理由.
【答案】见解析
【解析】先利用HL判定△AEC≌△BDE,从而得出全等三角形的对应角相等,再利用角与角之间的关系,可以得到线段CE与DE的大小与位置关系为相等且垂直.
解:(1)△AEC≌△BDE,理由为:
因为AC⊥AB,DB⊥AB,所以∠CAE=∠DBE=90°,
又因为AC=BE,AE=BD,所以△AEC≌△BDE.
(2)CE=DE,CE⊥DE,理由为:
由(1)可知,△AEC≌△BDE,所以CE=DE,∠C=∠DEB,
又因为在Rt△AEC中,∠C+∠CEA=90°,
所以∠DEB+∠CEA=90°,所以∠CED=90°,
所以CE⊥DE.
“点睛”本题考查了全等三角形的判定和性质,垂直的定义、平角的定义,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目