题目内容
【题目】如图，在平面直角坐标系中，抛物线y＝
与x轴交于A，C（A在C的左侧），点B在抛物线上，其横坐标为1，连接BC，BO，点F为OB中点．
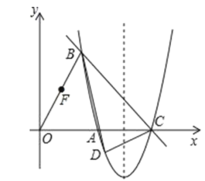
（1）求直线BC的函数表达式；
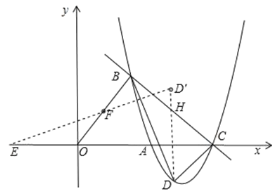
（2）若点D为抛物线第四象限上的一个动点，连接BD，CD，点E为x轴上一动点，当△BCD的面积的最大时，求点D的坐标，及|FE﹣DE|的最大值．
【答案】（1）y＝
x+
；（2）D（
，﹣
），|FE﹣DE|的最大值为
．
【解析】
（1）先求出B、C的坐标，利用待定系数法求解即可；
（2）三角形面积最值转换成求DH的最大值，然后利用二次函数的求最值问题解决点D的坐标，|FE﹣DE|的最大值，可将点D和点F转换到x轴的同一侧，再利用共线时差值最大求出线段长度即可．
（1）在y＝
中，当y＝0，解得：x1＝
，x2＝
，
∴A（，0），C（，0）
当x＝1时，y＝2
即B（1，2），
设直线BC的解析式为y＝kx+b
得：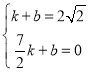
，
解得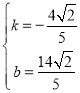
，
直线BC的解析式为y＝x+.
（2）设点D（m，
），则点H（m，m+）
过点D作DH⊥x轴交BC于点H，
HD＝m+﹣（）
＝
，
S△BCD=
×DH×（xC－xB）
=
DH，
∴当m＝时，HD取最大值，此时S△BCD的面积取最大值．
此时D（，﹣）.
作D关于x轴的对称点D′
则D′（，），
连接D′H交x轴于一点E，此时|D′E﹣FE|最大，最大值为D′F的长度，
∵F（，）
∴D′F＝，
即|FE﹣DE|的最大值为．
阅读快车系列答案
【题目】从甲地到乙地有A，B，C三条不同的公交线路．为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：
公交车用时 公交车用时的频数 线路 |
|
|
|
| 合计 |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
早高峰期间，乘坐_________（填“A”，“B”或“C”）线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大．
【题目】嘉善县将开展以“珍爱生命，铁拳护航”为主题的交通知识竞赛，某校对参加选拔赛的若干名同学的成绩按A，B，C，D四个等级进行统计，绘制成如下不完整的频数统计表和扇形统计图
成绩等级 | 频数（人数） | 频率 |
A | 4 | 0.08 |
B | m | 0.52 |
C | n | |
D | ||
合计 | 1 |
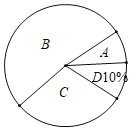
（1）求m＝ ，n＝ ；
（2）在扇形统计图中，求“C等级”所对应圆心角的度数；
（3）“A等级”的4名同学中有3名男生和1名女生，现从中随机挑选2名同学代表学校参加全县比赛，请用树状图法或列表法求出恰好选中“一男一女”的概率．
