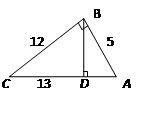题目内容
如图,三个村庄A、B、C之间的距离分别为AB=15km,BC=9km,AC=12km.已知A、B两村之间已修建了一条笔直的村级公路AB,为了实现村村通公路,现在要从C村修一条笔直公路CD直达AB.已知公路的造价为10000元/km,求修这条公路的最低造价是多少?
分析:首先得出BC2+AC2=92+122=225,AB2=152=225,然后利用其逆定理得到∠ACB=90°确定最短距离,然后利用面积相等求得CD的长,最终求得最低造价.
解答:解:∵BC2+AC2=92+122=225,
AB2=152=225,
∴BC2+AC2=AB2
∴∠ACB=90°
当CD⊥AB时CD最短,造价最低
∵S△ABC=
AC•BC=
AB•CD
∴CD=
=7.2
7.2×10000=72000元.
答:最低造价为72000元.
AB2=152=225,
∴BC2+AC2=AB2
∴∠ACB=90°
当CD⊥AB时CD最短,造价最低
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| AC•BC |
| AB |
7.2×10000=72000元.
答:最低造价为72000元.
点评:本题考查了勾股定理的应用,解题的关键是知道当什么时候距离最短.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
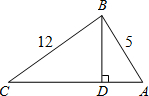 如图,三个村庄A、B、C之间的距离分别是AB=5km,BC=12km,AC=13km.要从B修一条公路BD直达AC.已知公路的造价为26000元/km,求修这条公路的最低造价是多少?
如图,三个村庄A、B、C之间的距离分别是AB=5km,BC=12km,AC=13km.要从B修一条公路BD直达AC.已知公路的造价为26000元/km,求修这条公路的最低造价是多少?