题目内容
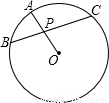
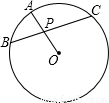
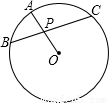
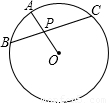
如图：若弦BC经过圆O的半径OA的中点P，且PB=3，PC=4，则圆O的直径为（ ）
A．7
B．8
C．9
D．10
【答案】分析：本题可根据相交弦定理求解，延长AO交⊙O于D，可用半径表示出AP，DP的长，根据相交弦定理可得：AP•PD=BP•PC，由此可求出⊙O的半径，进而可求出直径的长．
解答：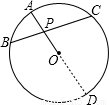
解：延长AO交⊙O于点D，
设⊙O的半径是x，
根据相交弦定理，得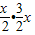
=12，x=4，
因此⊙O的直径是8．
故选B．
点评：注意延长半径构造相交弦，根据相交弦定理列方程求解．
解答：
解：延长AO交⊙O于点D，设⊙O的半径是x，
根据相交弦定理，得
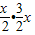=12，x=4，因此⊙O的直径是8．
故选B．
点评：注意延长半径构造相交弦，根据相交弦定理列方程求解．
练习册系列答案
相关题目
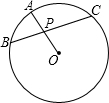如图：若弦BC经过圆O的半径OA的中点P，且PB=3，PC=4，则圆O的直径为（ ）| A、7 | B、8 | C、9 | D、10 |
