Question

某校九年级一班的暑假活动安排中，有一项是小制作评比．作品上交时限为8月1日至30日，班委会把同学们交来的作品按时间顺序每5天组成一组，对每一组的件数进行统计，绘制成如图所示的统计图．已知从左到右各矩形的高度比为2：3：4：6：4：1．第三组的频数是12．请你回答：
（1）本次活动共有

 

件作品参赛；
（2）上交作品最多的组有作品

 

件；
（3）经评比，第四组和第六组分别有10件和2件作品获奖，那么你认为这两组中哪个组获奖率较高？为什么？
（4）对参赛的每一件作品进行编号并制作成背面完全一致的卡片，背面朝上的放置，随机抽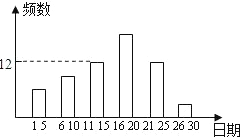出一张卡片，抽到第四组作品的概率是多少？

Answer 1

分析：（1）由于组距相同，各矩形的高度比即为频数的比，可由数据总数=某组的频数÷频率计算；
（2）第四组作品最多；
（3）分别计算第四、六组的获奖率后比较；
（4）根据概率公式计算．

解答：解：（1）12÷[4÷（2+3+4+6+4+1）]=60件；

（2）（12÷4）×6=18件；

（3）第四组获奖率

10

18

=

5

9

，第六组获奖率

2

3

=

6

9

，
又∵

5

9

＜

6

9

，
∴第六组获奖率高；

（4）P（第四组）=

18

60

=

3

10

，
∴抽到第四组作品的概率是

3

10

．

点评：此题考查了对频数分布直方图的掌握情况，根据图中信息，求出频率，用来估计概率．用到的知识点为：总体数目=部分数目÷相应频率．部分的具体数目=总体数目×相应频率．概率=所求情况数与总情况数之比．