Question

【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，3）．

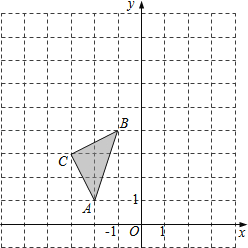
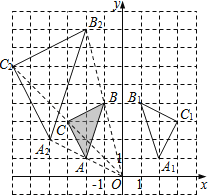
（1）画出△ABC关于y轴对称的△A1B1C1，并写出A1点的坐标及sin∠B1A1C1的值；

（2）以原点O为位似中心，位似比为1：2，在y轴的左侧，画出 将△ABC放大后的△A2B2C2，并写出A2点的坐标；

（3）若点D（a，b）在线段AB上，直接写出经过（2）的变化后点D的对应点D2的坐标．

Answer 1

【答案】（1）A1（2，1），； （2）A2（﹣4，2）；（3）D2（2a，2b）．

【解析】

试题分析：（1）利用关于y轴对称点的性质得出对应点坐标进而求出即可；

（2）利用位似图形的性质得出对应点位置即可得出答案；

（3）利用位似比得出对应点坐标的变化规律进而得出答案．

解：（1）如图，△A1B1C1，即为所求，

A1（2，1），

∵=B1C+A1C，A1C1=B1C1，

∴△A1B1C1是等腰直角三角形，

∴sin∠B1A1C1=sin45°=；

（2）如图，△A2B2C2，即为所求，

A2（﹣4，2）；

（3）∵点D（a，b）在线段AB上，位似比为1：2，

∴D2（2a，2b）．