Question

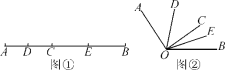
【题目】如图①，已知线段AB＝16 cm，点C为线段AB上的一个动点(点C不与A，B重合)，点D，E分别是AC和BC的中点．

(1)求DE的长；

(2)知识迁移：如图②，已知∠AOB＝130°，过角的内部任一点C画射线OC，若OD，OE分别平分∠AOC和∠BOC，试说明∠DOE的大小与射线OC的位置无关．

Answer 1

【答案】(1) 8 cm；(2) ∠DOE＝65°与射线OC位置无关，理由见解析.

【解析】

（1）由DE＝DC＋CE＝AC＋BC=AB得出即可；

（2）由∠DOE＝∠DOC＋∠EOC＝ (∠AOC＋∠BOC)＝∠AOB＝65°，与射线OC位置无关.

解：(1)∵点D，E分别是AC和BC的中点，

∴DC＝AC＝CE＝BC，

∴DE＝DC＋CE＝AC＋BC＝ (AC＋BC)＝×16＝8 cm；

(2)∵OD，OE分别平分∠AOC和∠BOC，

∴∠DOC＝∠AOC，∠EOC＝∠BOC，

∴∠DOE＝∠DOC＋∠EOC＝ (∠AOC＋∠BOC)＝∠AOB＝65°，

∴∠DOE＝65°与射线OC位置无关.