题目内容
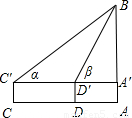
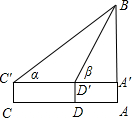 要测得底部不能到达的烟囱的高AB,从与烟囱底部在同一水平线的C、D两处测得烟囱的仰角为α、β,CD间的距离是a米,已知测角仪的高b米,求烟囱的高AB.
要测得底部不能到达的烟囱的高AB,从与烟囱底部在同一水平线的C、D两处测得烟囱的仰角为α、β,CD间的距离是a米,已知测角仪的高b米,求烟囱的高AB.
分析:在直角△A′BD′中,根据A′B和β可以求得A′D′的长度,在直角△A′BC′中,根据A′B和α可以求得A′C′的长度,根据B′C′=A′C′-A′D′即可求得A′B′的值,即可解题.
解答:解:在直角△A′BD′中,A′D′=A′B•cotβ
在直角△A′BC′中,A′C′=A′B•cotα
且C′D′=A′C′-A′D′,
∴C′D′=A′B(cotα-cotβ),
∴A′B=
.
∴AB=AA′+A′B=
+b.
在直角△A′BC′中,A′C′=A′B•cotα
且C′D′=A′C′-A′D′,
∴C′D′=A′B(cotα-cotβ),
∴A′B=
| a |
| cotα-cotβ |
∴AB=AA′+A′B=
| a |
| cotα-cotβ |
点评:本题考查了三角函数在直角三角形中的运用,本题中求A′C′和A′D′是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

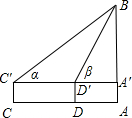 要测得底部不能到达的烟囱的高AB,从与烟囱底部在同一水平线的C、D两处测得烟囱的仰角为α、β,CD间的距离是a米,已知测角仪的高b米,求烟囱的高AB.
要测得底部不能到达的烟囱的高AB,从与烟囱底部在同一水平线的C、D两处测得烟囱的仰角为α、β,CD间的距离是a米,已知测角仪的高b米,求烟囱的高AB.