题目内容
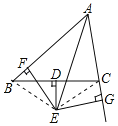
【题目】如图,在△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,AB=5,AC=3.求CG.

【答案】1
【解析】
连接BE、EC,证明Rt△EFB≌Rt△EGC,得出BF=CG,证明Rt△AEF≌Rt△AEG,得AF=AG,证出2AF=AB+AC,得出AG=AF=![]() (AB+AC)=4,即可得出答案.
(AB+AC)=4,即可得出答案.
解:连接BE、EC.
∵D为BC的中点,
∴BD=DC,
∵DE⊥BC,
∴EB=EC,
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴EF=EG,
在Rt△EFB和Rt△EGC中,![]() ,
,
∴Rt△EFB≌Rt△EGC(HL),
∴BF=CG.
在Rt△AEF和Rt△AEG中,![]() ,
,
∴Rt△AEF≌Rt△AEG(HL),
∴AF=AG,
∴AB+AC=AF+BF+AG﹣CG=2AF.
即2AF=AB+AC,
∴AG=AF=![]() (AB+AC)=
(AB+AC)=![]() (5+3)=4,
(5+3)=4,
∴CG=AG﹣AC=1.

练习册系列答案
相关题目