题目内容
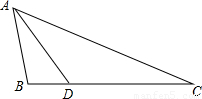
已知:如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.(1)求证:△ABD∽△CBA;
(2)若DE∥AB交AC于点E,请再写出另一个与△ABD相似的三角形,并直接写出DE的长.
【答案】分析:(1)在△ABD与△CBA中,有∠B=∠B,根据已知边的条件,只需证明夹此角的两边对应成比例即可;
(2)由(1)知△ABD∽△CBA,又DE∥AB,易证△CDE∽△CBA,则:△ABD∽△CDE,然后根据相似三角形的对应边成比例得出DE的长.
解答: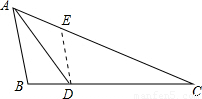 (1)证明:∵AB=2,BC=4,BD=1,
(1)证明:∵AB=2,BC=4,BD=1,
∴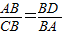 ,
,
∵∠ABD=∠CBA,
∴△ABD∽△CBA;
(2)解:∵DE∥AB,
∴△CDE∽△CBA,
∴△ABD∽△CDE,
∴DE=1.5.
点评:本题主要考查了相似三角形的判定及性质.平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;两组对应边的比相等且相应的夹角相等的两个三角形相似;相似三角形的对应边成比例.
(2)由(1)知△ABD∽△CBA,又DE∥AB,易证△CDE∽△CBA,则:△ABD∽△CDE,然后根据相似三角形的对应边成比例得出DE的长.
解答:
 (1)证明:∵AB=2,BC=4,BD=1,
(1)证明:∵AB=2,BC=4,BD=1,∴
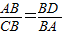 ,
,∵∠ABD=∠CBA,
∴△ABD∽△CBA;
(2)解:∵DE∥AB,
∴△CDE∽△CBA,
∴△ABD∽△CDE,
∴DE=1.5.
点评:本题主要考查了相似三角形的判定及性质.平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;两组对应边的比相等且相应的夹角相等的两个三角形相似;相似三角形的对应边成比例.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长. 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE. 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.