题目内容
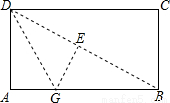
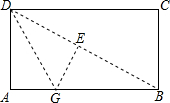 如图,折叠矩形的纸片ABCD,先折痕(对角线)DB,再过点D折叠,使AD落在折痕BD上,得另一折痕DG,若AB=2,BC=1,则AG=
如图,折叠矩形的纸片ABCD,先折痕(对角线)DB,再过点D折叠,使AD落在折痕BD上,得另一折痕DG,若AB=2,BC=1,则AG=
| ||
| 2 |
| ||
| 2 |
分析:在直角△ABG中,利用勾股定理即可求得BD的长,设AG=x,则在直角△BGE中利用勾股定理即可得到一个关于x的方程,求得AG的长.
解答:解:矩形ABCD中,AD=BC=DE=1,在直角△ABD中,BD=
=
=
,
设AG=x,则GE=AG=x.
在直角△BGE中,BE=BD-DE=
-1,BG=2-x.
根据勾股定理可得:BE2+GE2=BG2,即(
-1)2+x2=(2-x)2,
解得:x=
.
故答案是:
.
| AD2+AB2 |
| 1+4 |
| 5 |
设AG=x,则GE=AG=x.
在直角△BGE中,BE=BD-DE=
| 5 |
根据勾股定理可得:BE2+GE2=BG2,即(
| 5 |
解得:x=
| ||
| 2 |
故答案是:
| ||
| 2 |
点评:本题考查了矩形的性质,勾股定理,以及折叠的性质,正确利用线段长度之间的关系转化成方程问题是关键.

练习册系列答案
相关题目
 如图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,若AB=2,BC=1,求AG的长.
如图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,若AB=2,BC=1,求AG的长.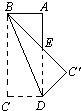 19、如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在C′处,BC'交AD于E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,则图中的等腰三角形有
19、如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在C′处,BC'交AD于E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,则图中的等腰三角形有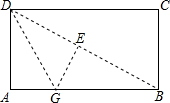 如图,折叠矩形的纸片ABCD,先折痕(对角线)DB,再过点D折叠,使AD落在折痕BD上,得另一折痕DG,若AB=2,BC=1,则AG=________.
如图,折叠矩形的纸片ABCD,先折痕(对角线)DB,再过点D折叠,使AD落在折痕BD上,得另一折痕DG,若AB=2,BC=1,则AG=________.