题目内容
一个不透明的口袋里装着三种球,它们只有颜色不同,其中红球有2个,黄球有1个,绿球的个数不清楚,从中任意摸出1球是红球的概率为
.
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出l球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,列举出所有可能出现的情况,并求出两次都摸到红球的概率.
| 1 | 2 |
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出l球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,列举出所有可能出现的情况,并求出两次都摸到红球的概率.
分析:(1)设绿球的个数是x,然后根据概率公式表示出红球的个数列出方程,然后进行计算即可得解;
(2)画出树状图,然后根据概率公式列式进行计算即可得解.
(2)画出树状图,然后根据概率公式列式进行计算即可得解.
解答:解:(1)设绿球的个数是x,
根据题意得,
(2+1+x)=2,
解得x=1,
答:袋中绿球的个数是1;
(2)画树状图如图:
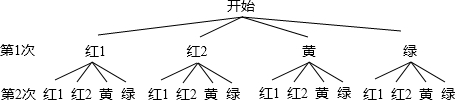
一共有16种情况,两次都摸到红球的情况数有4种,
所以,P(两次都摸到红球)=
=
.
根据题意得,
| 1 |
| 2 |
解得x=1,
答:袋中绿球的个数是1;
(2)画树状图如图:

一共有16种情况,两次都摸到红球的情况数有4种,
所以,P(两次都摸到红球)=
| 4 |
| 16 |
| 1 |
| 4 |
点评:本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 .
. .
.