题目内容
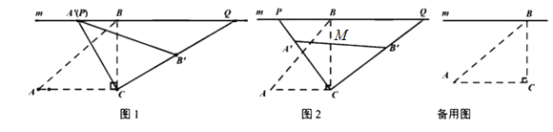
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,
上一点,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 中点,
中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,
,![]() ≌
≌![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的大小;
的大小;
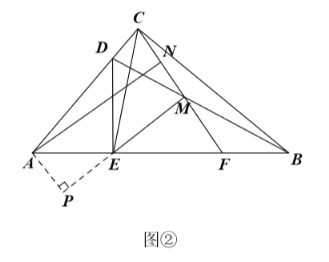
(3)如图②,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:四边形
,求证:四边形![]() 为矩形.
为矩形.
【答案】(1)证明见解析;(2)∠MEF=30°;(3)证明见解析.
【解析】
(1)利用直角三角形斜边中线的性质定理可得CM=![]() DB,EM=
DB,EM=![]() DB,问题得证;
DB,问题得证;
(2)利用全等三角形的性质,证明△DEM是等边三角形,即可解决问题;
(3)设FM=a,则AE=CM=EM=![]() a,EF=2a,推出
a,EF=2a,推出![]() ,
,![]() ,得到AN∥PM,易证四边形ANMP是平行四边形,结合∠P=90°即可解决问题.
,得到AN∥PM,易证四边形ANMP是平行四边形,结合∠P=90°即可解决问题.
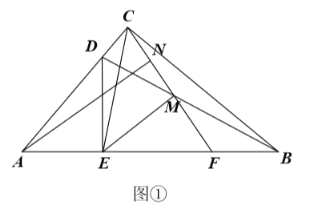
解:(1)证明:如图①中,
∵DE⊥AB,
∴∠DEB=∠DCB=90°,
∵DM=MB,
∴CM=![]() DB,EM=
DB,EM=![]() DB,
DB,
∴CM=EM;
(2)解:∵△DAE≌△CEM,CM=EM,
∴AE=ED=EM=CM=DM,∠AED=∠CME=90°
∴△ADE是等腰直角三角形,△DEM是等边三角形,
∵∠AED=∠DEF=90°,∠DEM=60°,
∴∠MEF=30°;
(3)证明:如图②中,设FM=a.
由(2)可知△ADE是等腰直角三角形,△DEM是等边三角形,∠MEF=30°,
∴AE=CM=EM=![]() a,EF=2a,
a,EF=2a,
∵CN=NM,
∴MN=![]() a,
a,
∴![]() ,
,![]() ,
,
∴EM∥AN,
∵AP⊥PM,MN⊥PM,
∴AP∥MN,
∴四边形ANMP是平行四边形,
∵∠P=90°,
∴四边形ANMP是矩形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目