题目内容
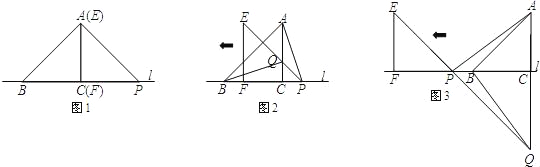
【题目】锐角为45°的直角三角形的两直角边长也相等,这样的三角形称为等腰直角三角形.我们常用的三角板中有一块就是这样的三角形,也可称它为等腰直角三角板.把两块全等的等腰直角三角板按如图1放置,其中边BC、FP均在直线l上,边EF与边AC重合.
(1)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(2)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
【答案】见解析
【解析】试题分析:(1)延长BQ交AP于点M,根据等腰直角三角板的每一个锐角都是45°可得∠EPF=45°,然后求出∠CQP=45°,根据等角对等边的性质求出CQ=CP,然后利用边角边定理证明△BCQ与△ACP全等,再根据全等三角形对应边相等,即可证明BQ=AP,对应角相等可得∠CBQ=∠CAP,又∠CBQ+∠BQC=90°,所以∠CAP+∠AQM=90°,从而得到BQ⊥AP;
(2)延长QB交AP于点M,根据等腰直角三角板的每一个锐角都是45°可得∠EPF=45°,根据对顶角相等得到∠CPQ=45°,然后求出∠CQP=45°,根据等角对等边的性质求出CQ=CP,然后利用边角边定理证明△BCQ与△ACP全等,再根据全等三角形对应边相等,即可证明BQ=AP,对应角相等可得∠BQC=∠APC,又∠CBQ+∠BQC=90°,所以∠PBM+∠APC=90°,从而得到BQ⊥AP.
试题解析:(1)BQ=AP,BQ⊥AP.
证明:延长BQ交AP于点M,
∵△ABC和△EFP都是等腰直角三角板,
∴BC=AC,AC⊥BC,∠EPF=45°,
∴∠BCQ=∠ACP=90°,∠CQP=∠EPF=45°,
∴CQ=CP,
在△BCQ和△ACP中,
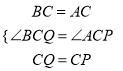 ,
,
∴△BCQ≌△ACP(SAS),
∴BQ=AP,∠CBQ=∠CAP,
∵∠BCQ=90°,
∴∠CBQ+∠BQC=90°,
∵∠BQC=∠AQM(对顶角相等),
∴∠CAP+∠AQM=90°,
∴∠AMB=90°,
∴BQ⊥AP;
(2)关系仍然成立:BQ=AP,BQ⊥AP.
证明:延长QB交AP于点M,
∵△ABC和△EFP都是等腰直角三角板,
∴BC=AC,AC⊥BC,∠EPF=45°,
∴∠BCQ=∠ACP=90°,
∵∠CQP=∠EPF=45°,
∴∠CPQ=∠CQP=45°,
∴CQ=CP,
在△BCQ和△ACP中,
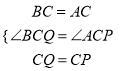 ,
,
∴△BCQ≌△ACP(SAS),
∴BQ=AP,∠BQC=∠APC,
∵∠BCQ=90°,
∴∠CBQ+∠BQC=90°,
∵∠PBM=∠QBC(对顶角相等),
∴∠PBM+∠APC=90°.

 名校课堂系列答案
名校课堂系列答案