题目内容
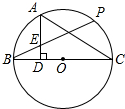 如图,已知BC是⊙O的直径,P是⊙O上一点,A是
如图,已知BC是⊙O的直径,P是⊙O上一点,A是 |
| BP |
(1)求
 |
| AB |
(2)求证:AE=BE.
分析:(1)要求
的长,就要连接OA,求出圆心角,利用弧长公式计算;
(2)连接AB,点A是
的中点,所以
=
,则利用等弧所对的圆周角相等可得∠C=∠ABP.在Rt△ABD和Rt△ADC中,利用同一角的余角相等可得∠BAD=∠C,则∠ABP=∠BAD,所以AE=BE.
 |
| AB |
(2)连接AB,点A是
 |
| BP |
 |
| BA |
 |
| AP |
解答: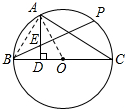 (1)解:连接OA,∵∠ACB=36°,∴∠AOB=72°.
(1)解:连接OA,∵∠ACB=36°,∴∠AOB=72°.
又∵OB=
BC=5,
∴
的长为:l=
=
=2π.
(2)证明:连接AB,
∵点A是
的中点,
∴
=
.
∴∠C=∠ABP.
∵BC为⊙O的直径,
∴∠BAC=90°,即∠BAD+∠CAD=90°,
又∵AD⊥BC,
∴∠C+∠CAD=90°,
∴∠BAD=∠C,
∴∠ABP=∠BAD,
∴AE=BE.
 (1)解:连接OA,∵∠ACB=36°,∴∠AOB=72°.
(1)解:连接OA,∵∠ACB=36°,∴∠AOB=72°.又∵OB=
| 1 |
| 2 |
∴
 |
| AB |
| nπR |
| 180 |
| 72×π×5 |
| 180 |
(2)证明:连接AB,
∵点A是
 |
| BP |
∴
 |
| BA |
 |
| AP |
∴∠C=∠ABP.
∵BC为⊙O的直径,
∴∠BAC=90°,即∠BAD+∠CAD=90°,
又∵AD⊥BC,
∴∠C+∠CAD=90°,
∴∠BAD=∠C,
∴∠ABP=∠BAD,
∴AE=BE.
点评:本题主要考查了弧长公式和等弧所对的圆周角相等的性质.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 7、如图,已知BC是⊙O的直径,AD切⊙O于A,若∠C=40°,则∠DAC=( )
7、如图,已知BC是⊙O的直径,AD切⊙O于A,若∠C=40°,则∠DAC=( )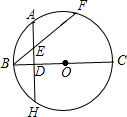 如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为
如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为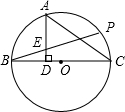 如图,已知BC是⊙O的直径,P是⊙O上一点,A是
如图,已知BC是⊙O的直径,P是⊙O上一点,A是 (2013•宁德质检)如图,已知BC是⊙O的直径,AB是⊙O的切线,AO交⊙O于点D,∠A=28°,则∠C=
(2013•宁德质检)如图,已知BC是⊙O的直径,AB是⊙O的切线,AO交⊙O于点D,∠A=28°,则∠C=