题目内容
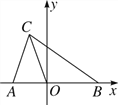
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且![]() +(4a-b+11)2=0.
+(4a-b+11)2=0.
(1)求a,b的值;
(2)在y轴的负半轴上存在一点M,使△COM的面积等于△ABC面积的一半,求出点M的坐标.
【答案】(1)a的值是-2,b的值是3;(2)M的坐标是(0,-![]() ).
).
【解析】试题分析:(1)根据![]() +(4a-b+11)2=0,可得
+(4a-b+11)2=0,可得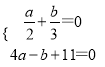 ,据此求出a、b的值即可.
,据此求出a、b的值即可.
(2)首先过点C作CG⊥x轴,CH⊥y轴,垂足分别为G、H,然后根据三角形的面积的求法,求出△ABC的面积,再用它除以2,求出△COM的面积是多少,进而求出点M的坐标即可.
试题解析:(1)∵![]() +(4a-b+11)2=0,
+(4a-b+11)2=0,
∴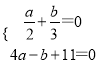
解得![]()
∴ a的值是-2,b的值是3.
(2) 如图1,过点C作CG⊥x轴,CH⊥y轴,垂足分别为G、H,
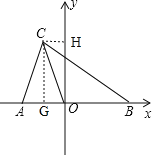
∵A(-2,0),B(3,0),
∴AB=3-(-2)=5,
∵点C的坐标是(-1,3),
∴CG=3,CH=1,
∴S△ABC=![]() ABAC=
ABAC=![]() ×5×3=
×5×3=![]() ,
,
∴S△COM=![]() ,
,
即![]() OMCH=
OMCH=![]() ,
,
∴OM=![]() =7.5,
=7.5,
∴点M的坐标是(0,-7.5).

练习册系列答案
相关题目
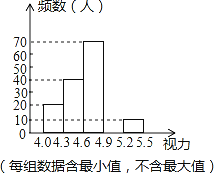
【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?