题目内容
 (2013•海沧区一模)已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.
(2013•海沧区一模)已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.(1)求证:FD是⊙O的切线;
(2)设OC与BE相交于点G,若OG=4,求⊙O半径的长;
(3)在(2)的条件下,当OE=6时,求图中阴影部分的面积.(结果保留根号)
分析:(1)连接OC.欲证FD是⊙O的切线,只需证明OC⊥CD即可;
(2)由条件可以知道E是AC的中点,O是AB的中点,就可以得出G是△ABC的重心,根据三角形的重0)定理就可以求出OC的长得出其结论.
(3)由条件可以求出sin∠ACO=
,就可以求出∠ACO=30°,可以求出∠DOC=60°,从而求出CD的值,求出S△DOC的面积,求出扇形COB的面积就可以求出阴影部分的面积.
(2)由条件可以知道E是AC的中点,O是AB的中点,就可以得出G是△ABC的重心,根据三角形的重0)定理就可以求出OC的长得出其结论.
(3)由条件可以求出sin∠ACO=
| 1 |
| 2 |
解答:解: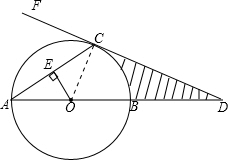 (1)证明:连接OC.
(1)证明:连接OC.
∵OA=OC(⊙O的半径),
∴∠CAO=∠ACO(等边对等角),即∠EA0=∠ECO,
又∵OE⊥AC,
∴∠CEO=∠AEO=90°,
∴∠AOE=∠COE,∠EOC+∠OCE=90°,
∴∠AOE+∠OCE=90°,
∵∠FCA=∠AOE,
∴∠FCA+∠OCE=90°.
即∠FCO=90°.
∴OC⊥DF,
∴FD是⊙O的切线;
(2)连接BE交OC于G,
∵OE⊥AC,
∴AE=CE,
∵AO=BO,
∴G是△ABC的重心,
∴CG=2GO.
∵GO=4,
∴CG=8,
∴OC=8+4=12.
∴⊙O半径的长为12.
(3)∵OE⊥AC,OE=6,OC=12,
∴sin∠ACO=
,
∴∠ACO=30°,
∴∠A=30°,
∴∠COD=60°,
∵OC⊥CD,
∴∠OCD=90°,
∴tan∠COD=tan60°=
=
,且OC=12,
∴CD=12
.
∴S△COD=12×12
÷2=72
.
S扇形COB=
=24π,
∴阴影部分的面积为:72
-24π.
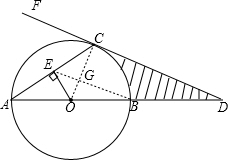
 (1)证明:连接OC.
(1)证明:连接OC.∵OA=OC(⊙O的半径),
∴∠CAO=∠ACO(等边对等角),即∠EA0=∠ECO,
又∵OE⊥AC,
∴∠CEO=∠AEO=90°,
∴∠AOE=∠COE,∠EOC+∠OCE=90°,
∴∠AOE+∠OCE=90°,
∵∠FCA=∠AOE,
∴∠FCA+∠OCE=90°.
即∠FCO=90°.
∴OC⊥DF,
∴FD是⊙O的切线;
(2)连接BE交OC于G,
∵OE⊥AC,
∴AE=CE,
∵AO=BO,
∴G是△ABC的重心,
∴CG=2GO.
∵GO=4,
∴CG=8,
∴OC=8+4=12.
∴⊙O半径的长为12.
(3)∵OE⊥AC,OE=6,OC=12,
∴sin∠ACO=
| 1 |
| 2 |
∴∠ACO=30°,
∴∠A=30°,
∴∠COD=60°,
∵OC⊥CD,
∴∠OCD=90°,
∴tan∠COD=tan60°=
| 3 |
| CD |
| OC |
∴CD=12
| 3 |
∴S△COD=12×12
| 3 |
| 3 |
S扇形COB=
| 60×π×144 |
| 360 |
∴阴影部分的面积为:72
| 3 |

点评:本题试一道有关圆的综合试题,考查了切线的判定及性质,三角函数的值的运用,垂径定理的运用,三角形的面积,扇形的面积的运用.在解答中注意辅助线的运用.

练习册系列答案
相关题目
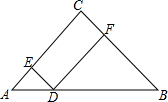 (2013•海沧区一模)如图,在等腰直角三角形ABC中,AC=BC=2,D为AB上的动点(不与A,B重合),过D作DE⊥AC于E,DF⊥BC于F,设AD的长度为x,DE与DF的长度和为y.则能表示y与x之间的函数关系的图象大致是( )
(2013•海沧区一模)如图,在等腰直角三角形ABC中,AC=BC=2,D为AB上的动点(不与A,B重合),过D作DE⊥AC于E,DF⊥BC于F,设AD的长度为x,DE与DF的长度和为y.则能表示y与x之间的函数关系的图象大致是( )