题目内容
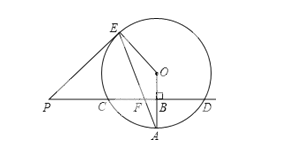
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
【答案】(1)、CD=8![]() ;(2)、证明过程见解析.
;(2)、证明过程见解析.
【解析】
试题分析:(1)、连接OD,根据垂径定理可得:OB=4,OD=8,根据Rt△OBD的勾股定理求出BD的长度,然后求出CD的长度;(2)、根据切线性质可得∠PEO=90°,根据OA=OE得出∠A=∠AEO,根据∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A得出∠PEF=∠PFE,从而得出PE=PF.
试题解析:(1)、连接OD,∵直线PD垂直平分⊙O的半径OA于点B,⊙O的半径为8,
∴OB=![]() OA=4,BC=BD=
OA=4,BC=BD=![]() CD, ∴在Rt△OBD中,BD=
CD, ∴在Rt△OBD中,BD=![]() =4
=4![]() , ∴CD=2BD=8
, ∴CD=2BD=8![]() ;
;
(2)、∵PE是⊙O的切线, ∴∠PEO=90°,
∴∠PEF=90°﹣∠AEO,∠PFE=∠AFB=90°﹣∠A,
∵OE=OA, ∴∠A=∠AEO, ∴∠PEF=∠PFE, ∴PE=PF;

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
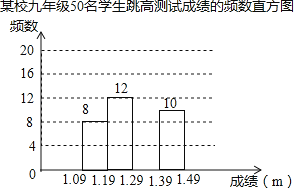
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.